論理数学 - 写像
ナビゲーションに移動
検索に移動
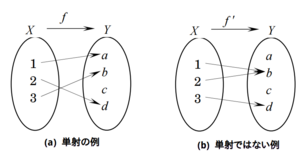
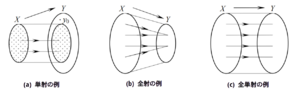
図(a). 単射の例
図(b). 単射でない例 図(a). 全射の例
図(b). 全射でない例 図(a). 単射の例
図(b). 全射の例
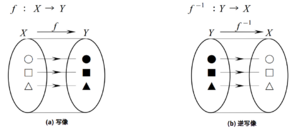
図(c). 全単射の例 図(a). 写像
図(b). 逆写像 図. 像・逆像のイメージ 図. 像・逆像の例 図. 写像の合成
概要
写像 (関数) とは、ある集合Aの全ての要素に対して、集合Bの要素をただ1つ返すものである。
この時、集合Aを始域または定義域、集合Bを終域、関数の対応先となり得る集合𝐵の部分集合を値域という。
写像の定義
定義 : 集合Aの全ての要素に対して、その要素を入力すると集合Bの特定の要素をただ1つ出力するものを関数 (function) または 写像 (mapping) という。 この時、集合Aをその写像の始域または定義域 (domain) といい、集合Bを終域 (codomain) という。 また、集合Aを入力したときの出力となり得る集合Bの部分集合全体を関数 (写像) の値域 (像 range) という。
写像についての注意点を、以下に示す。
- 始域Aの全ての要素において、終域Bの要素をただ1つ返すこと。
- 始域Bの要素であれば、どの要素を返してもよい。
始域Aの各々の要素に対して、終域Bの同じ要素を返してもよい。
また、終域Bの全ての要素を対応付ける必要はない。 - 終域は、値域と呼ばれることもある。
恒等写像
定義 : 集合X上の写像 (定義域Xと終域Xが同一である写像) において、 に対して が成り立つ時、 を 上の恒等写像という。 補足 : は、集合Xの任意の要素aという意味である。
写像の表記
写像は関数 (function) の頭文字を用いて、と表記されることが多い。
2つ以上の写像がある場合は、アルファベット順に 等と表記する。
始域が集合A、終域が集合Bである写像 を、 と記述する。
集合Aの各要素 に対して、それに対応する集合Bの要素が であるとき、これを または と記述する。
また,終域・値域は、 と記述する。
写像の例
は実数全体の集合、 は整数全体の集合を表す。
例題 1: があるとする。 この写像は、英語の小文字を入力する時、その大文字を出力する。 この時、 であり、終域・値域は である。
例題 2: があるとする。 この写像は、整数を入力する時、2で剰余した値を出力する。 この時、 であり、値域は である。
例題 3: があるとする。 この写像は、 と定義する。 この時、 であり、値域は である。
単射
定義 : 始域Xから終域Yへの写像fが に対して、常に を満たす時、 写像fは単射 (1対1対応) であるという。 補足 : 対偶 に対して、常に を満たす、と同義である。
図(b). 単射でない例
全射
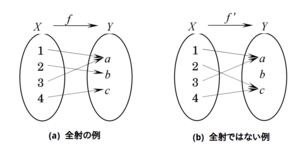
定義 : 始域Xから終域Yへの写像fについて、 に対して、常に を満たす要素 が存在する時、 写像fは全射(上への対応)であるという。
図(b). 全射でない例
全単射
定義 : 全射であり、かつ、単射である写像を全単射 (上への1対1対応) という。
図(b). 全射の例
図(c). 全単射の例
逆写像
定義 : 集合Xから集合Yへの写像fが全単射である時、 に対して、 を満たす要素 を対応させる写像をfの逆写像といい、 で表す。
図(b). 逆写像
例 : の逆写像 とおき、xについて解く。 したがって、 一般的に、写像はxの式で表すので、yをxに置き換えて次式のように表す。
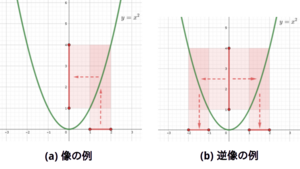
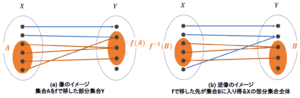
逆像
定義 : 始域Xから終域Yへの写像 とYの部分集合Bが与えられた時、
Xの部分集合 をfによるBの逆像という。
補足 : 多価写像に対しても、上と同様に逆像が定義される。
例 : を とする。 この時、 である。
また、 である。
恒等写像
全ての元を同じものに写す写像を恒等写像とよぶ。
定義 : 写像 が、任意の に対して を満たす時、fを恒等写像という。 この時、 と記述することがある。
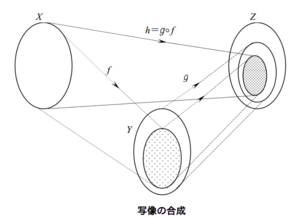
写像の合成
定義 : 写像 と写像 に対して、 で定められる写像 をfとgの合成写像といい、 で表す。
補足 : 写像の合成は、合成の順序に依存することに注意する。 例 : の時、







































![{\displaystyle f([1,\,2])=[1,\,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3fa0e073870f3cc0b48048d5d86a3c76ab220f9)
![{\displaystyle f^{-1}([1,\,4])=[-2,\,-1]\cup [1,\,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f969df573abd2fc64a95d1575561fcb57ae10068)