第2回 グラフの基礎概念と例
概要
グラフの基礎概念
- グラフの同形
- グラフG1とG2が同形である。 ⇔ G1とG2の点の間に1対1対応があり、G1の任意の2点を結ぶ辺数がG2の対応する2点を結ぶ辺数に等しい。
- 次数と握手補題
- 次数 : 点に接続している辺の本数である。
- 握手補題 : 任意のグラフのすべての点の次数を合計すれば偶数になる。
- 行列を用いたグラフの表現法
- 隣接行列 : 点iとjを結ぶ辺の本数をij要素とする行列。
- 接続行列 : 点iが辺jに接続しているときij要素が1、接続していないとき0であるような行列。
グラフの例
- 完全グラフ : 相異なる2つの点がすべて隣接している単純グラフ。n個の点をもつ完全グラフをKnと表す。
Knには、本の辺がある。 - 正則グラフ : どの点の次数も同じであるグラフ。次数がrであるとき、r-正則グラフと呼ばれる。
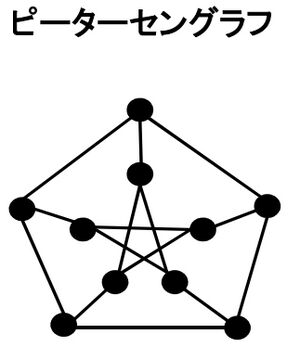
- ピーターセングラフ
- プラトングラフ
- 2部グラフ : グラフGの点集合を、互いに同じ要素を持たない集合AとBに分割し、Gの全ての辺はAの点とBの点を結ぶようにしたグラフ。
- 完全2部グラフ
- k-立方体
単純グラフ
単純グラフ(simple graph)とは、多重辺やループを含まないグラフのことである。
で表される。
V(G)は、点、頂点または節点と呼ばれる元からなる空でない有限集合である。
E(G)は、辺と呼ばれる元からなる有限集合である。辺はV(G)の異なる2点の非順序対である。
V(G)はGの点集合と呼ばれ、E(G)はGの辺集合と呼ばれる。
辺{v, w}は、点vと点wを結ぶと言い、vwと略記される。
例
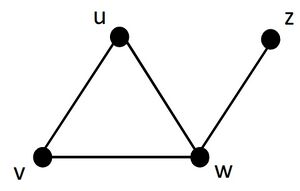
下図は単純グラフGを表す。
- Gの点集合
- Gの辺集合
一般グラフ
単純グラフにおいて、以下の2つを考慮したグラフを一般グラフ(general graph)あるいは単にグラフという。
- 2つの点を結ぶ辺が2本以上であることを許す。
- どの辺も2つの相異なる点を結ぶという制約を外し、同じ点を結ぶ辺(ループ)の存在を許す。
一般グラフの定義
一般グラフGは、点と呼ばれる元からなる空でない有限集合V(G)と、
辺と呼ばれるV(G)の(必ずしも相異なるとは限らない)元の非順序対からなる有限な多重集合であるE(G)からなる。
V(G)をGの点集合、E(G)を辺多重集合と呼ぶ。
多重集合とは、同じ元が複数個あることを認める集合のことである。{a, a, a, b, c, c}
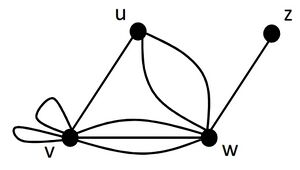
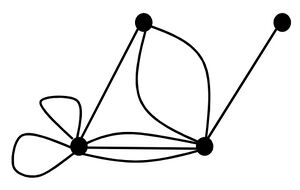
下図は、一般グラフGを表す。
同形(同型)
2つのグラフG1とG2の点の間に1対1対応があり、G1の任意の2点を結ぶ辺数がG2の対応する2点を結ぶ辺数に等しいとき、
G1とG2は同形(isomorphic)であるという。
グラフが同形か否かを調べるためには、2つのグラフの各点にラベルを付けて、
それら2つのグラフ間の各点のラベルの対応を調べる。
例
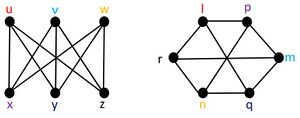
下図の2つのグラフは同形である。
点の対応 : u ⇔ l、v ⇔ m、w ⇔ n、x ⇔ p、y ⇔ q、z ⇔ r
同形の判定法
- グラフGとHが同形であることを示す方法
- Hの点の名前を付け替えるとGになる。
- Hの点のいくつかを移動するとGと同じ形になる。
- グラフGとHが同形でないことを示す方法
- Gの点の名前をどのように変えてもHにならないことを示す。名前の付け方をすべて試す必要があり、難しい。
- 2つのグラフの特徴を見て、異なる特徴を挙げる。
- グラフ間における異なる特徴の例
- 点の数や辺の数が違えば同形ではない。
- 点と辺の数がそれぞれ同じでも、次数列が異なれば同形ではない。次数列については後述する。
- 点のつながり方が違えば同形ではない。
- 一方に長さkのサイクルがあり、他方になければ同形ではない。
グラフの和
2つのグラフを考える。
ここで、V(G1)とV(G2)は共通の要素を持たないとする。
このとき、G1とG2の和は、
点集合と辺集合を持つグラフである。
例
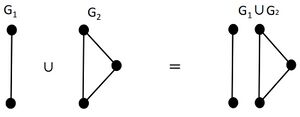
下図に、グラフG1とG2の和を示す。
連結・非連結グラフ
2つのグラフの和として表現できないグラフは、連結と呼ばれる。
2つのグラフの和として表現できるグラフは非連結と呼ばれる。
連結なグラフを連結グラフという。
非連結なグラフを非連結グラフという。
任意の非連結グラフGは連結グラフの和として表せる。このとき、各々の連結グラフはGの成分と呼ばれる。
例
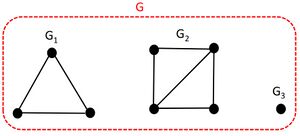
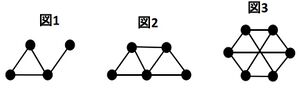
下図に、3つの成分G1、G2、G3からなる非連結グラフGを示す。
隣接
- 点の隣接
- グラフGに2つの点vとwを結ぶ辺vwがあるとき、vとwは隣接しているという。
- このとき、点vとwは辺vwに接続しているという。
- 辺の隣接
- 同様に、グラフGの2本の辺が1つの点を共有しているとき、その2辺は隣接しているという。
例
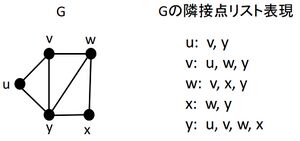
下図に、単純グラフGの隣接点をリストする方法を示す。
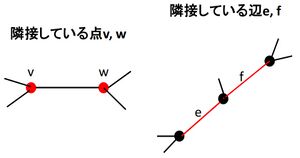
隣接している点v、wと隣接している辺e、fを示す。
単純グラフの表現法
単純グラフの別な表現法として以下の2つがある。
- 表現法1
- 隣接点をリストする方法。グラフの各点に隣接している点をリストにする。
- 下図に、単純グラフGの隣接点をリストする方法を示す。
- 表現法2
- 行列を使用する方法。隣接行列と接続行列を使用する。
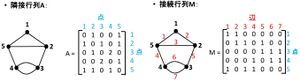
- 下図に、隣接行列を使用する方法を示す。
- 単純グラフGの点が{1, 2, ..., n}とラベル付けされているとき、
- 単純グラフGの隣接行列Aとは、点iとjを結ぶ辺の本数をij要素とするn×n行列である。
- 下図に、接続行列を使用する方法を示す。
- 単純グラフGについて、更に、辺が{1, 2, ..., m}とラベル付けされているとき、
- 単純グラフGの接続行列Mとは、点iが辺jに接続しているときij要素が1であり、接続していないとき0であるようなn×m行列である。
次数と次数列
グラフGの点vの次数は、vに接続している辺の本数である。点vの次数はdeg(v)で表す。
グラフの各点の次数を増加順に、必要ならば同じ次数を繰り返し表したものを、グラフの次数列という。
次数を計算するときには、vの1つのループは2本として計算する。
次数0の点は孤立点と呼ばれ、次数1の点は端点と呼ばれる。
例
下図のグラフには、端点が1個、次数3の点が1個、次数6の点が1個、次数8の点が1個ある。
下図のグラフの次数列は、(1, 3, 6, 8)である。
握手補題
補題 : 任意のグラフのすべての点の次数を合計すれば偶数になる。
グラフの各辺は2本あるので、全ての点の合計は辺数の2倍である。
部分グラフ
部分グラフ(sub graph)とは、その点はすべてV(G)に属し、その辺はすべてE(G)に属すグラフのことである。
グラフの辺と点を除去して部分グラフを作ることができる。
例
下図Aのグラフは、下図Bのグラフの部分グラフである。
下図Aのグラフは、下図Cのグラフの部分グラフではない。下図Cのグラフには、点と辺により作られる三角形が含まれないため。
辺と点の除去
- 辺の除去(1)
- eがグラフGの辺であるとき、Gから辺eを除去して得られるグラフをG - eと書く。
- 辺の除去(2)
- グラフGの辺の集合の部分集合をFとしたとき、GからFの辺をすべて除去して得られるグラフをG - Fと書く。
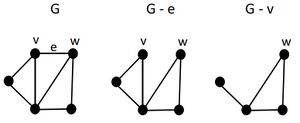
- 点と辺の除去(1)
- 同様にして、グラフGから点vおよびvに接続する辺すべてを除去して得られるグラフをG - vと書く。
- 点と辺の除去(2)
- SがGの点の集合の部分集合であるとき、Sの点とそれらに接続している全ての辺を除去して得られるグラフをG - Sと書く。
例
辺の縮約
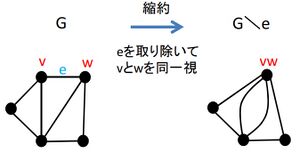
グラフGから、辺eを除去し、その端点vとwを同一視して1点にすることを、グラフGの辺eに対する縮約(contraction)という。
即ち、端点vまたはwに接続していた(辺e以外)の辺を新しくできた点に接続させたグラフである。
グラフGの辺eに対する縮約グラフを、と書く。
例
下図に、グラフGの辺eに対する縮約グラフを示す。
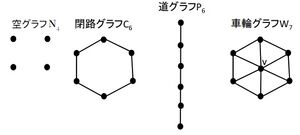
空グラフ 閉路グラフ 道グラフ 車輪グラフ
- 空グラフ(Null graph)
- 辺集合が空であるグラフのことである。空グラフでは、すべての点が孤立点である。
- m個の点の空グラフを、Nnと表す。下図に、空グラフN4を示す。
- 閉路グラフ(cycle graph)
- 全ての点の次数が2の連結グラフを閉路グラフという。
- n個の点をもつ閉路グラフを、Cnと書く。
- 道グラフ(path graph)
- Cnから1つの辺を除いて得られるグラフを、n個の点をもつ道グラフという。
- n個の点をもつ道グラフを、Pnと書く。
- 車輪グラフ(wheel graph)
- Cn - 1に1つの新しい点vを加え、点vと他の全ての点とを辺で結んで得られるグラフを、n点の車輪グラフという。
- n点の車輪グラフをWnと書く。
例
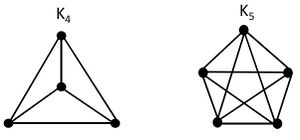
完全グラフ
完全グラフ(Complete graph)とは、相異なる2つの点がすべて隣接している単純グラフのことである。
n個の点をもつ完全グラフをKnと表す。完全グラフKnには、本の辺がある。
例
正則グラフ
正則グラフ(Regular graph)とは、どの点の次数も同じであるグラフのことである。
次数がrであるとき、次数rの正則グラフあるいはr-正則グラフという。
特に、彩色問題で重要となるのは、次数3の正則グラフである。このグラフは、3次(cubic)グラフともいう。
3次グラフの中で有名な例として、ピーターセングラフがある。
例
空グラフNnは次数0の正則グラフである。
閉路グラフCnは次数2の正則グラフである。
完全グラフKnは次数n - 1の正則グラフである。
正則グラフの一種として、プラトングラフがある。プラトングラフは正多面体(プラトンの多面体)の頂点と辺から作られたグラフである。
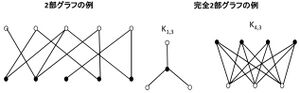
2部グラフと完全2部グラフ
2部グラフ
2部グラフとは、グラフGの点集合を、互いに同じ要素をもたない集合AとBに分割し、
グラフGの全ての辺は集合Aの点と集合Bの点を結ぶようにしたグラフ。
グラフGの各点が黒の点(Aの要素)と白の点(Bの要素)を結ぶように、グラフGの点を黒と白で塗れるとき、Gは2部グラフである。
完全2部グラフ
完全2部グラフとは、グラフGの点集合を、互いに同じ要素をもたない集合AとBに分割したとする。
このとき、Aの各点がBの各点と1本の辺で結ばれている2部グラフを、完全2部グラフという。
黒の点(Aの要素)をr個、白の点(Bの要素)をs個をもつ2部グラフをKr, sと書く。
2部グラフKr, sには、r + s個の点とr×s本の辺がある。
例
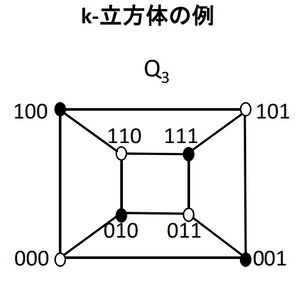
k-立方体
k-立方体(k-cube)とは、またはであるような1つの列に1つの点を対応させたグラフであり、
1個だけ異なるaiをもつ2つの列に対応する2つの点が辺で結ばれる。
k-立方体を、Qkと書く。
Qkは、2k個の点とk2k - 1本の辺をもつ次数kの正則2部グラフである。
立方体のグラフはQ3である。
例
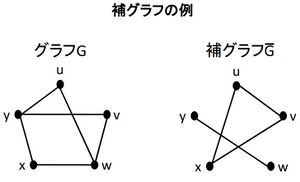
単純グラフの補グラフ
単純グラフGの補グラフ(Complement graph)Gとは、Gと同じ点集合V(G)をもち、
Gの2点が隣接するのはGにおけるそれら2点が隣接していないときかつそのときに限るような単純グラフである。
補グラフは、相補グラフともいう。
完全グラフの補グラフは空グラフである。
完全2部グラフの補グラフは2つの完全グラフの和である。
例