|
|
| 71行目: |
71行目: |
| <br> | | <br> |
| 上三角行列と下三角行列を総称して三角行列とよぶ。<br> | | 上三角行列と下三角行列を総称して三角行列とよぶ。<br> |
| | <br><br> |
| | |
| | == 行列の性質 == |
| | ==== 単位行列の行列式 ==== |
| | <math>\det E = 1</math><br> |
| | <br> |
| | <math> |
| | |E| = |
| | \begin{vmatrix} |
| | 1 & 0 & 0 \\ |
| | 0 & 1 & 0 \\ |
| | 0 & 0 & 1 |
| | \end{vmatrix} |
| | = 1 |
| | </math><br> |
| | <br> |
| | ==== 交代性 ==== |
| | <math>\det (a, b) = - \det (b, a)</math><br> |
| | <br> |
| | <math> |
| | A = (a, b) = |
| | \begin{pmatrix} |
| | 1 & 2 \\ |
| | 3 & 4 |
| | \end{pmatrix} |
| | \qquad |
| | \begin{vmatrix} |
| | 1 & 2 \\ |
| | 3 & 4 |
| | \end{vmatrix} |
| | = - |
| | \begin{vmatrix} |
| | 2 & 1 \\ |
| | 4 & 3 |
| | \end{vmatrix} |
| | = -2 |
| | </math> |
| | <br> |
| | ==== 多重線形性 ==== |
| | <math>\det (a_{1} + a_{2}, b) = \det (a_{1}, b) + \det (a_{2}, b)</math><br> |
| | <math>\det (ka, b) = k \times \det (a, b)</math><br> |
| | <br> |
| | <math> |
| | |A| = |
| | \begin{vmatrix} |
| | 2 & 0 & 3 \\ |
| | 2 & 1 & 0 \\ |
| | 2 & 1 & 2 |
| | \end{vmatrix} |
| | = |
| | 2 \times |
| | \begin{vmatrix} |
| | 1 & 0 & 3 \\ |
| | 1 & 1 & 0 \\ |
| | 1 & 1 & 2 |
| | \end{vmatrix} |
| | = 4 |
| | </math> |
| <br><br> | | <br><br> |
|
| |
|
| __FORCETOC__ | | __FORCETOC__ |
| [[カテゴリ:線形代数]] | | [[カテゴリ:線形代数]] |
2021年8月13日 (金) 08:31時点における版
概要
ここでは、行列の基本変形の意味とその応用(rankや行列式の求め方)について記載する。
行基本変形
以下の3つの操作を行基本変形という。
- 操作 1 : i行目とj行目を交換する。
- 操作 2 : i行目をc倍する。(c≠0)
- 操作 3 : j行目のc倍をi行目に加える。
列基本変形
行の場合と同様に、以下の3つの操作を列基本変形という。
- 操作 1 : i列目とj列目を交換する。
- 操作 2 : i列目をc倍する。(c≠0)
- 操作 3 : j列目のc倍をi列目に加える。
列基本変形は、正則行列を右から乗算することに対応している。(行基本変形の場合と同様に説明できる)
行基本変形と正則行列
行基本変形は、正則行列を左から乗算することに対応している。
操作1から順に説明していく。
操作 1
単位行列のi行とj行を交換した行列P(i, j)を左から乗算することに対応している。
例えば、 を3×3の行列
を3×3の行列 に左から乗算すると、
に左から乗算すると、 となり、
となり、
2行目と3行目が交換される。
なお、P(i,j)の行列式は、−1なので正則である。
操作2
単位行列のii成分をcとした行列P(i;c)を左から乗算することに対応している。
例えば、 を
を に左から乗算すると、
に左から乗算すると、 となり、2行目が6倍される。
となり、2行目が6倍される。
なお、P(i;c)の行列式はcなので正則である。
操作3
単位行列のij成分をcとした行列P(i,j;c)を左から乗算することに対応している。
例えば、 を
を に左から乗算すると、
に左から乗算すると、 となり、
となり、
3行目の6倍が2行目に加算される。
なお、P(i,j;c)の行列式は1なので正則である。
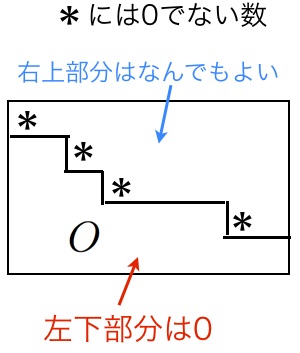
行基本変形でrankを求める
与えられた行列に対して、行基本変形を繰り返す(適当な正則行列を左から乗算する)ことで、下図のような階段形にすることができる。
正則行列を乗算してもrankは変わらないので、この階段形の行列のrankは元の行列のrankと一致する。
そして、階段形の行列のrankは一瞬で求まる。(0でない成分がある行の数)
行基本変形で行列式を求める
与えられた正方行列Aに対して、行基本変形を繰り返す(適当な正則行列Sを左から乗算する)ことで、階段形R(上三角行列)にすることができる。
つまり、 である。
である。
したがって、 であり、
であり、
- detRは、対角成分の積で簡単に求まる。
- detSも、変形の過程を見れば分かる。(操作2のcの積)
ので、detAが求まる。
備考 : 上三角行列と下三角行列
n×nの正方行列 に於いて、
に於いて、
 ならば
ならば を満たす行列を上三角行列
を満たす行列を上三角行列
 ならば
ならば を満たす行列を下三角行列
という。
を満たす行列を下三角行列
という。
上三角行列は、対角成分よりも下側の成分が0である行列である。
3×3の例 : 
下三角行列は、対角成分よりも上側の成分が0である行列である。
3×3の例 : 
上三角行列と下三角行列を総称して三角行列とよぶ。
行列の性質
単位行列の行列式


交代性


多重線形性