「畳み込み積分」の版間の差分
ナビゲーションに移動
検索に移動
(→概要) |
(→概要) |
||
| 5行目: | 5行目: | ||
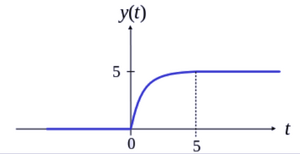
<math>y(t) = \int_{- \infty}^{\infty} {f(\tau)g(t - \tau)} d \tau</math><br> | <math>y(t) = \int_{- \infty}^{\infty} {f(\tau)g(t - \tau)} d \tau</math><br> | ||
<br> | <br> | ||
<math>y(t) = f(t)*g(t) \ | <math>y(t) = f(t)*g(t) \, \,</math> あるいは <math>\, \, y = f * g</math> と記述されることもある。<br> | ||
<br> | <br> | ||
また、以下に示すように、畳み込み積分は可換である。<br> | また、以下に示すように、畳み込み積分は可換である。<br> | ||






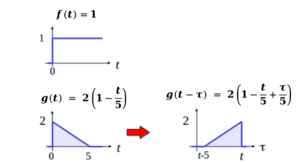








![{\displaystyle {\begin{aligned}y(t)&=\int _{0}^{1}{f(\tau )g(t-\tau )}d\tau \\&=\int _{0}^{1}{f(\tau )g(1-\tau )}d\tau \\&=\int _{0}^{1}{2(1-{\frac {1}{5}}+{\frac {\tau }{5}})}d\tau \\&=2\left[{\frac {4}{5}}\tau +{\frac {\tau ^{2}}{10}}\right]_{0}^{1}\\&=2\left({\frac {4}{5}}+{\frac {1}{10}}\right)\\&={\frac {9}{5}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9ffd88d284a8b6953b35e86a3b588bf6aec75a4)

![{\displaystyle {\begin{aligned}y(t)&=\int _{0}^{5}{f(\tau )g(t-\tau )}d\tau \\&=\int _{0}^{5}{f(\tau )g(5-\tau )}d\tau \\&=\int _{0}^{5}{2(1-1+{\frac {\tau }{5}})}d\tau \\&=2\left[{\frac {\tau ^{2}}{10}}\right]_{0}^{5}\\&=2{\frac {5}{2}}\\&=5\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee10e860cde010036a1f5fe88dbf037e908e2c10)

![{\displaystyle {\begin{aligned}y(t)&=\int _{0}^{t}{2(1-{\frac {t}{5}}+{\frac {\tau }{5}})}d\tau \\&=2\left[\tau -{\frac {t}{5}}\tau +{\frac {\tau ^{2}}{10}}\right]_{0}^{t}\\&=2\left(t-{\frac {t^{2}}{5}}+{\frac {t^{2}}{10}}\right)\\&=2t-{\frac {t^{2}}{5}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d57bd98e200a231499c580c3a100c1502c34ece0)