「回路計算 - 鳳テブナンの定理」の版間の差分
| (同じ利用者による、間の4版が非表示) | |||
| 27行目: | 27行目: | ||
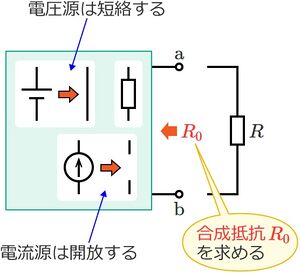
# 回路内の全ての電源を取り除き(電圧源は短絡して、電流源は開放する)、端子a-bからみた回路の合成抵抗R<sub>0</sub>を求める。 | # 回路内の全ての電源を取り除き(電圧源は短絡して、電流源は開放する)、端子a-bからみた回路の合成抵抗R<sub>0</sub>を求める。 | ||
#: [[ファイル:Tebnan Theorem 7.jpg|フレームなし|中央]] | #: [[ファイル:Tebnan Theorem 7.jpg|フレームなし|中央]] | ||
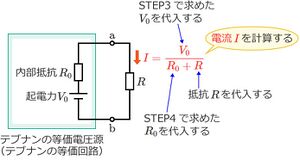
# 上記3で求めた開放電圧V<sub>0</sub>と、上記4で求めた合成抵抗R<sub>0</sub>を、テブナンの定理の式 <math>I = \frac{V_0}{R_0 + R}に代入して、電流Iを計算する。 | # 上記3で求めた開放電圧V<sub>0</sub>と、上記4で求めた合成抵抗R<sub>0</sub>を、テブナンの定理の式 <math>I = \frac{V_0}{R_0 + R}</math> に代入して、電流Iを計算する。 | ||
#: [[ファイル:Tebnan Theorem 8.jpg|フレームなし|中央]] | #: [[ファイル:Tebnan Theorem 8.jpg|フレームなし|中央]] | ||
<br> | <br> | ||
| 36行目: | 36行目: | ||
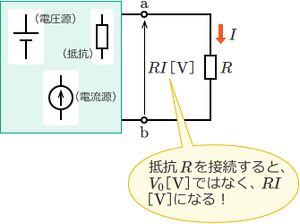
<u>抵抗Rを接続した状態では、抵抗Rに掛かる電圧は、V<sub>0</sub>[V]ではなくRI[V]になることに注意する。</u><br> | <u>抵抗Rを接続した状態では、抵抗Rに掛かる電圧は、V<sub>0</sub>[V]ではなくRI[V]になることに注意する。</u><br> | ||
[[ファイル:Tebnan Theorem 9.jpg|フレームなし|中央]] | [[ファイル:Tebnan Theorem 9.jpg|フレームなし|中央]] | ||
<br><br> | |||
== テブナンの定理による電流の計算例 == | |||
==== 電源が1つ、抵抗が3つある回路 ==== | |||
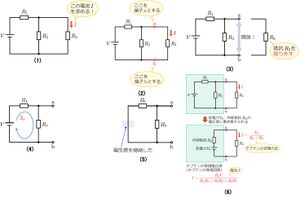
テブナンの定理を用いて、下図(1)の回路の抵抗R<sub>3</sub>に流れる電流Iを求める。<br> | |||
[[ファイル:Tebnan Theorem 10.jpg|フレームなし|中央]] | |||
<br> | |||
まず、抵抗R<sub>3</sub>に流れる電流を求めるため、上図(2)のように、抵抗R<sub>3</sub>の両端を端子a、bとする。<br> | |||
上図(3)のように、抵抗R<sub>3</sub>を取り外して、端子a-b間を開放状態にする。<br> | |||
上図(4)のように、端子a-b間に現れる電圧(開放電圧)V<sub>0</sub>を求める。<br> | |||
上図(4)の回路に流れる電流I<sub>0</sub>、および、端子a-b間の電圧(開放電圧)V<sub>0</sub>は、次式となる。<br> | |||
<math>I_0 = \frac{V}{R_1 + R_2} \quad \mbox{よ り } \quad \quad V_0 = \frac{R_2}{R_1 + R_2} V</math><br> | |||
<br> | |||
上図(5)のように、電圧源を短絡および電流源は開放して、端子a-bからみた回路の合成抵抗R<sub>0</sub>を求める。<br> | |||
電源を取り除くと、抵抗R<sub>1</sub>と抵抗R<sub>2</sub>が並列に接続された回路になるため、端子a-bからみた回路の合成抵抗R<sub>0</sub>は次式となる。<br> | |||
<math>R_0 = \frac{R_1 R_2}{R_1 + R_2}</math><br> | |||
<br> | |||
上記で求めた開放電圧V<sub>0</sub>および合成抵抗R<sub>0</sub>をテブナンの定理の式に代入して、電流Iを計算する。(上図(6))<br> | |||
<math> | |||
\begin{align} | |||
I &= \frac{V_0}{R_0 + R_3} \\ | |||
&= \frac{\frac{R_2}{R_1 + R_2} V}{\frac{R_1 R_2}{R_1 + R_2} + R_3} \\ | |||
&= \frac{R_2}{R_1 R_2 + R_3 R_1 + R_3 R_2} V | |||
\end{align} | |||
</math><br> | |||
<br> | |||
==== 電源が2つ、抵抗が3つある回路 ==== | |||
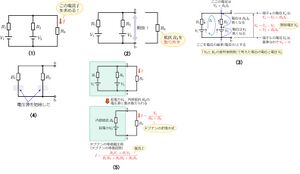
テブナンの定理を用いて、下図(1)の回路の抵抗R<sub>3</sub>に流れる電流Iを求める。<br> | |||
[[ファイル:Tebnan Theorem 11.jpg|フレームなし|中央]] | |||
<br> | |||
まず、抵抗R<sub>3</sub>に流れる電流を求めるため、上図(2)のように、抵抗R<sub>3</sub>の両端を端子a、bとする。<br> | |||
抵抗R3を取り外して、端子a-b間を開放状態にする。<br> | |||
上図(3)のように、端子a-b間に現れる電圧(開放電圧)V<sub>0</sub>を求める。<br> | |||
<math>V_1 - V_2 = R_1 I_0 + R_2 I_0</math><br> | |||
<math>V_1 - V_2 = (R_1 + R_2) I_0</math><br> | |||
<math>I_0 = \frac{V_1 - V_2}{R_1 + R_2}</math><br> | |||
<br> | |||
<math> | |||
\begin{align} | |||
V_0 &= V_2 + R_2 I_0 \\ | |||
&= V_2 + R_2 \frac{V_1 - V_2}{R_1 + R_2} \\ | |||
&= \frac{V_2 (R_1 + R_2)}{R_1 + R_2} + \frac{R_2 (V_1 - V_2)}{R_1 + R_2} \\ | |||
&= \frac{V_2 (R_1 + R_2) + R_2 (V_1 - V_2)}{R_1 + R_2} \\ | |||
&= \frac{R_1 V_2 + R_2 V_1}{R_1 + R_2} | |||
\end{align} | |||
</math><br> | |||
<br> | |||
上図(4)のように、電圧源は短絡および電流源は開放して、端子a-bからみた回路の合成抵抗R<sub>0</sub>を求める。<br> | |||
<math>R_0 = \frac{R_1 R_2}{R_1 + R_2}</math><br> | |||
<br> | |||
端子a-b間の抵抗R<sub>3</sub>、および、上記で求めた開放電圧V<sub>0</sub>および合成抵抗R<sub>0</sub>をテブナンの定理の式に代入して、電流Iを計算する。(上図(5))<br> | |||
<math> | |||
\begin{align} | |||
I &= \frac{V_0}{R_0 + R_3} \\ | |||
&= \frac{\frac{R_2 V_1 + R_1 V_2}{R_1 + R_2}}{\frac{R_1 R_2}{R_1 + R_2} + R_3} \\ | |||
&= \frac{R_2 V_1 + R_1 V_2}{R_1 R_2 + R_3 (R_1 + R_2)} \\ | |||
&= \frac{R_2 V_1 + R_1 V_2}{R_1 R_2 + R_3 R_1 + R_3 R_2} | |||
\end{align} | |||
</math><br> | |||
<br><br> | <br><br> | ||
__FORCETOC__ | __FORCETOC__ | ||
[[カテゴリ:回路計算]] | [[カテゴリ:回路計算]] | ||
2022年6月1日 (水) 14:57時点における最新版
概要
鳳テブナンの定理(等価電圧源の定理とも呼ばれる)とは、電源を含む回路において、ある特定の素子に流れる電流を求めたい場合に有用な定理である。
鳳テブナンの定理とは
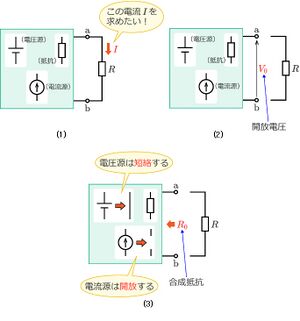
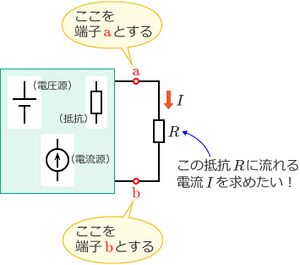
例えば、下図(1)のような電源を含む回路があって、この回路の端子a-b間に接続されている抵抗R[Ω]に流れる電流I[A]を求めたいとする。
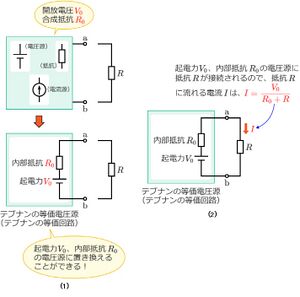
この時、抵抗Rを取り外した状態での端子a-b間に現れる電圧(開放電圧)をV0[V]、抵抗Rを取り外した状態での端子a-b間の合成抵抗をR0[Ω]とすると、
端子a-bより左側の回路は、起電力がV0、内部抵抗がR0の電圧源に置き換える(等価変換する)ことができ、抵抗Rに流れる電流Iは、次式で求めることができる。
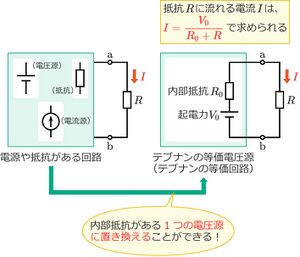
鳳テブナンの定理を用いると、電流を求めたい箇所の特定の素子を除いた部分の回路(上図の場合、端子a-bより左側の回路)を、内部抵抗がある1つの電圧源として等価的に置き換えることができる。
そのため、複雑な回路であっても、回路を単純化して電流を計算することができる。
鳳テブナンの定理による電流の求め方
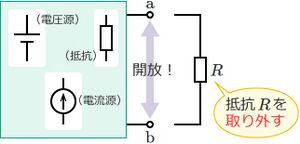
- 電流を求めたい抵抗Rの両端を端子a、bとする。
- 抵抗Rを取り外して、端子a-b間を開放状態にする。
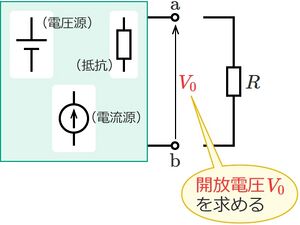
- 端子a-b間に現れる電圧(開放電圧)V0を求める。
- 回路内の全ての電源を取り除き(電圧源は短絡して、電流源は開放する)、端子a-bからみた回路の合成抵抗R0を求める。
- 上記3で求めた開放電圧V0と、上記4で求めた合成抵抗R0を、テブナンの定理の式 に代入して、電流Iを計算する。
以上の手順で、抵抗Rに流れる電流Iを求めることができる。
※補足
上記3で求めた開放電圧はV0[V]であるが、この電圧V0[V]は抵抗Rを接続して抵抗Rに電流が流れている状態での抵抗Rの両端にかかる電圧(端子a-b間の電圧)とは異なる。
抵抗Rを接続した状態では、抵抗Rに掛かる電圧は、V0[V]ではなくRI[V]になることに注意する。
テブナンの定理による電流の計算例
電源が1つ、抵抗が3つある回路
テブナンの定理を用いて、下図(1)の回路の抵抗R3に流れる電流Iを求める。
まず、抵抗R3に流れる電流を求めるため、上図(2)のように、抵抗R3の両端を端子a、bとする。
上図(3)のように、抵抗R3を取り外して、端子a-b間を開放状態にする。
上図(4)のように、端子a-b間に現れる電圧(開放電圧)V0を求める。
上図(4)の回路に流れる電流I0、および、端子a-b間の電圧(開放電圧)V0は、次式となる。
上図(5)のように、電圧源を短絡および電流源は開放して、端子a-bからみた回路の合成抵抗R0を求める。
電源を取り除くと、抵抗R1と抵抗R2が並列に接続された回路になるため、端子a-bからみた回路の合成抵抗R0は次式となる。
上記で求めた開放電圧V0および合成抵抗R0をテブナンの定理の式に代入して、電流Iを計算する。(上図(6))
電源が2つ、抵抗が3つある回路
テブナンの定理を用いて、下図(1)の回路の抵抗R3に流れる電流Iを求める。
まず、抵抗R3に流れる電流を求めるため、上図(2)のように、抵抗R3の両端を端子a、bとする。
抵抗R3を取り外して、端子a-b間を開放状態にする。
上図(3)のように、端子a-b間に現れる電圧(開放電圧)V0を求める。
上図(4)のように、電圧源は短絡および電流源は開放して、端子a-bからみた回路の合成抵抗R0を求める。
端子a-b間の抵抗R3、および、上記で求めた開放電圧V0および合成抵抗R0をテブナンの定理の式に代入して、電流Iを計算する。(上図(5))