「回路計算 - 合成インピーダンス」の版間の差分
(→例題 2) |
|||
| (同じ利用者による、間の17版が非表示) | |||
| 1行目: | 1行目: | ||
== 概要 == | == 概要 == | ||
回路の受動素子(抵抗R、コイルL、コンデンサC)が直列接続または並列接続されている場合の合成インピーダンスの計算手順を記載する。<br> | |||
<br><br> | |||
== RL直列回路の合成インピーダンス == | |||
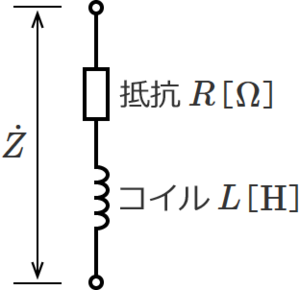
RL直列回路は、抵抗RとコイルLが直列に接続された回路で、下図のような回路になる。<br> | |||
[[ファイル:CircuitCalc Synthetic Impedance 5.png|フレームなし|中央]] | |||
<center>図.1 抵抗RとコイルLが直列接続の回路</center><br> | |||
<br> | |||
直列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、それぞれのインピーダンスを加算することにより求められる。<br> | |||
<br> | |||
RL直列回路の合成インピーダンス<math>\dot{Z}</math>は、次式で与えられる。<br> | |||
なお、角周波数<math>\omega = 2 \pi f</math>である。<br> | |||
<br> | |||
* 複素数表示の場合 | |||
<math>\dot{Z} = R + j \omega L \quad [\Omega]</math><br> | |||
<br> | |||
<math>\omega \ge 0, \quad R > 0, \quad L > 0</math>であるため、<math>\Re(Z) = R > 0, \quad \Im(Z) = \omega L > 0</math>となり、<br> | |||
RL直列回路の合成インピーダンス<math>\dot{Z}</math>のベクトルの向きは、必ず右上向き(複素数平面の第1象限)になる。<br> | |||
<br> | |||
* 合成インピーダンスの大きさの場合 | |||
<math> | |||
\begin{align} | |||
\dot{Z} &= R + j \omega L \\ | |||
\left | Z \right | &= \sqrt{R^2 + (\omega L)^2} \quad [\Omega] | |||
\end{align} | |||
</math><br> | |||
<br><br> | |||
== RC直列回路の合成インピーダンス == | |||
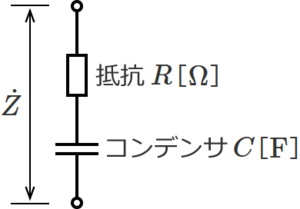
RC直列回路は、抵抗RとコンデンサCが直列に接続された回路で、下図のような回路になる。<br> | |||
[[ファイル:CircuitCalc Synthetic Impedance 6.png|フレームなし|中央]] | |||
<center>図.2 抵抗RとコンデンサCが直列接続の回路</center><br> | |||
<br> | |||
直列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、それぞれのインピーダンスを加算することにより求められる。<br> | |||
<br> | |||
RC直列回路の合成インピーダンス<math>\dot{Z}</math>は、次式で与えられる。<br> | |||
なお、角周波数<math>\omega = 2 \pi f</math>である。<br> | |||
<br> | |||
* 複素数表示の場合 | |||
<math> | |||
\begin{align} | |||
\dot{Z} &= R + \frac{1}{j \omega C} \\ | |||
&= R - j \frac{1}{\omega C} \quad [\Omega] | |||
\end{align} | |||
</math><br> | |||
<br> | |||
<math>\omega \ge 0, \quad R > 0, \quad C > 0</math>であるため、<br> | |||
<math>\Re(Z) = R > 0, \quad \Im(Z) = - \frac{1}{\omega C} < 0</math>となり、<br> | |||
RC直列回路の合成インピーダンス<math>\dot{Z}</math>のベクトルの向きは、必ず右下向き(複素数平面の第4象限)になる。<br> | |||
<br> | |||
* 合成インピーダンスの大きさの場合 | |||
<math> | |||
\begin{align} | |||
\dot{Z} &= R + \frac{1}{j \omega C} \\ | |||
&= R - j \frac{1}{\omega C} \\ | |||
\left | Z \right | &= \sqrt{R^2 + \left (\frac{1}{\omega C} \right )^2} \quad [\Omega] | |||
\end{align} | |||
</math><br> | |||
<br><br> | |||
== LC直列回路の合成インピーダンス == | |||
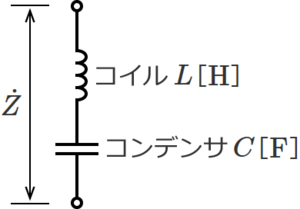
LC直列回路は、抵抗RとコンデンサCが直列に接続された回路で、下図のような回路になる。<br> | |||
[[ファイル:CircuitCalc Synthetic Impedance 7.png|フレームなし|中央]] | |||
<center>図.3 コイルLとコンデンサCが直列接続の回路</center><br> | |||
<br> | |||
直列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、それぞれのインピーダンスを加算することにより求められる。<br> | |||
<br> | |||
LC直列回路の合成インピーダンス<math>\dot{Z}</math>は、次式で与えられる。<br> | |||
なお、角周波数<math>\omega = 2 \pi f</math>である。<br> | |||
<br> | |||
* 複素数表示の場合 | |||
<math> | |||
\begin{align} | |||
\dot{Z} &= j \omega L + \frac{1}{j \omega C} \\ | |||
&= j \omega L - j \frac{1}{\omega C} \\ | |||
&= j \left (\omega L - \frac{1}{\omega C} \right ) \quad [\Omega] | |||
\end{align} | |||
</math><br> | |||
<br> | |||
<math>\omega \ge 0, \quad L > 0, \quad C > 0</math>であるため、<br> | |||
<math>\Re(Z) = 0, \quad -\infty < \Im(Z) = - \frac{1}{\omega C} < \infty</math>となり、<br> | |||
LC直列回路の合成インピーダンス<math>\dot{Z}</math>のベクトルの向きは、必ず、虚数軸上となる。<br> | |||
<br> | |||
LC直列回路の合成インピーダンス<math>\dot{Z}</math>は、上式の分母が正・負・ゼロの時、それぞれ<math>\dot{Z}</math>のベクトルの向きが変わる。<br> | |||
したがって、<math>1 - \omega^2 LC > 0, \quad 1 - \omega^2 LC < 0, \quad 1 - \omega^2 LC = 0</math>の時で、場合分けして考える必要がある。<br> | |||
* <math>\omega L - \frac{1}{\omega C} > 0</math>の場合 | |||
*: 上式のリアクタンスが正になるため、合成インピーダンスのベクトルは、虚数軸上の正の向きになる。 | |||
*: <br> | |||
* <math>\omega L - \frac{1}{\omega C} < 0</math>の場合 | |||
*: 上式のリアクタンスが負になるため、合成インピーダンスのベクトルは、虚数軸上の負の向きになる。 | |||
*: <br> | |||
* <math>\omega L - \frac{1}{\omega C} = 0</math>の場合 | |||
*: 上式のリアクタンスが0になるため、合成インピーダンスのベクトルは、複素数平面の原点Oとなる。 | |||
*: インピーダンスが0ということは、その回路は短絡状態と同じになる。 | |||
*: <br> | |||
*: また、<math>\omega L - \frac{1}{\omega C} = 0</math> すなわち、<math>\omega = \frac{1}{\sqrt{LC}}</math> は、回路の共振条件である。 | |||
<br> | |||
* 合成インピーダンスの大きさの場合 | |||
<math> | |||
\begin{align} | |||
\dot{Z} &= j \omega L + \frac{1}{j \omega C} \\ | |||
&= j \left (\omega L - \frac{1}{\omega C} \right ) \\ | |||
\left | Z \right | &= \sqrt{\left (\omega L - \frac{1}{\omega C} \right )^2} \\ | |||
&= \left | \omega L - \frac{1}{\omega C} \right | \quad [\Omega] | |||
\end{align} | |||
</math><br> | |||
<br><br> | |||
== RLC直列回路の合成インピーダンス == | |||
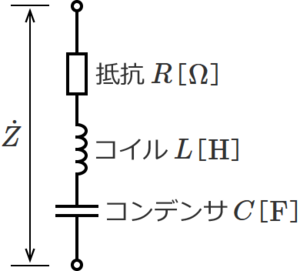
RLC並列回路は、抵抗R、コイルL、コンデンサCが並列に接続された回路で、下図のような回路になる。<br> | |||
[[ファイル:CircuitCalc Synthetic Impedance 8.png|フレームなし|中央]] | |||
<center>図.4 抵抗R、コイルL、コンデンサCが直列接続の回路</center><br> | |||
<br> | |||
直列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、それぞれのインピーダンスを加算することにより求められる。<br> | |||
<br> | |||
RLC直列回路の合成インピーダンス<math>\dot{Z}</math>は、次式で与えられる。<br> | |||
なお、角周波数<math>\omega = 2 \pi f</math>である。<br> | |||
<br> | |||
* 複素数表示の場合 | |||
<math> | |||
\begin{align} | |||
\dot{Z} &= \dot{Z_1} + \dot{Z_2} + \dot{Z_3} = R + j \omega L + \frac{1}{j \omega C} \\ | |||
&= R + j \omega L - j \frac{1}{\omega C} \\ | |||
&= R + j (\omega L - \frac{1}{\omega C}) \quad [\Omega] | |||
\end{align} | |||
</math><br> | |||
<br> | |||
<math>\omega \ge 0, \quad R > 0, \quad L > 0, \quad C > 0</math>であるため、<br> | |||
<math>\Re(Z) = R > 0, \quad -\infty < \Im(Z) = \omega L - \frac{1}{\omega C} < \infty</math>となり、<br> | |||
RLC直列回路の合成インピーダンス<math>\dot{Z}</math>のベクトルの向きは、複素数平面の右上(第1象限)または右下(第4象限)または実数軸上となる。<br> | |||
<br> | |||
RLC直列回路の合成インピーダンス<math>\dot{Z}</math>は、上式の虚部(<math>\omega L - \frac{1}{\omega C}</math>)が正・負・ゼロの時、それぞれ<math>\dot{Z}</math>のベクトルの向きが変わる。<br> | |||
したがって、<math>\omega L - \frac{1}{\omega C} > 0, \quad \omega L - \frac{1}{\omega C} < 0, \quad \omega L - \frac{1}{\omega C} = 0</math>の時で、場合分けして考える必要がある。<br> | |||
* <math>\omega L - \frac{1}{\omega C} > 0</math> の場合 | |||
*: 上式のリアクタンスが正になるため、合成インピーダンスのベクトルは、右上の向き(第1象限)になる。 | |||
*: <br> | |||
* <math>\omega L - \frac{1}{\omega C} < 0</math> の場合 | |||
*: 上式のリアクタンスが負になるため、合成インピーダンスのベクトルは、右下の向き(第4象限)になる。 | |||
*: <br> | |||
* <math>\omega L - \frac{1}{\omega C} = 0</math> の場合 | |||
*: 上式のリアクタンスが0になるため、合成インピーダンスのベクトルは、実数軸上の正の向きになる。(<math>\dot{Z} = R [\Omega]</math>) | |||
*: この条件を満たす周波数は共振周波数であるため、コイルLとコンデンサCの直列回路部分は短絡状態と同じになる。 | |||
*: <br> | |||
*: また、<math>\omega L - \frac{1}{\omega C} = 0</math> すなわち、<math>\omega = \frac{1}{\sqrt{LC}}</math> は、回路の共振条件である。 | |||
<br> | |||
* 合成インピーダンスの大きさの場合 | |||
<math> | |||
\begin{align} | |||
\dot{Z} &= R + j \omega L + \frac{1}{j \omega C} \\ | |||
&= R + j (\omega L - \frac{1}{\omega C}) \\ | |||
\left | Z \right | &= \sqrt{R^2 + \left ( \omega L - \frac{1}{\omega C} \right )^2} \quad [\Omega] | |||
\end{align} | |||
</math><br> | |||
<br><br> | <br><br> | ||
| 6行目: | 158行目: | ||
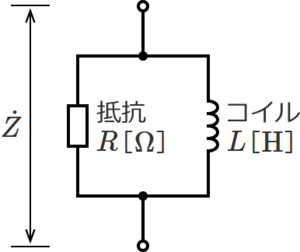
RL並列回路は、抵抗RとコイルLが並列に接続された回路で、下図のような回路になる。<br> | RL並列回路は、抵抗RとコイルLが並列に接続された回路で、下図のような回路になる。<br> | ||
[[ファイル:CircuitCalc Synthetic Impedance 1.png|フレームなし|中央]] | [[ファイル:CircuitCalc Synthetic Impedance 1.png|フレームなし|中央]] | ||
<center>図. | <center>図.5 抵抗RとコイルLが並列接続の回路</center><br> | ||
<br> | <br> | ||
並列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、<br> | 並列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、<br> | ||
| 44行目: | 196行目: | ||
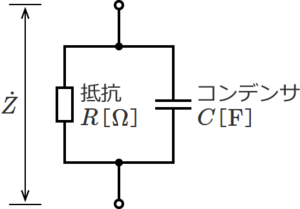
RC並列回路は、抵抗RとコンデンサCが並列に接続された回路で、下図のような回路になる。<br> | RC並列回路は、抵抗RとコンデンサCが並列に接続された回路で、下図のような回路になる。<br> | ||
[[ファイル:CircuitCalc Synthetic Impedance 2.png|フレームなし|中央]] | [[ファイル:CircuitCalc Synthetic Impedance 2.png|フレームなし|中央]] | ||
<center>図. | <center>図.6 抵抗RとコンデンサCが並列接続の回路</center><br> | ||
<br> | <br> | ||
並列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、<br> | 並列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、<br> | ||
| 65行目: | 217行目: | ||
<br> | <br> | ||
<math>\omega \ge 0, \quad R > 0, \quad C > 0</math>であるため、<br> | <math>\omega \ge 0, \quad R > 0, \quad C > 0</math>であるため、<br> | ||
<math>\Re(Z) = \frac{R}{1 + (\omega RC)^2} > 0, \quad \Im(Z) = \frac{\omega R^2 C}{1 + (\omega RC)^2} | <math>\Re(Z) = \frac{R}{1 + (\omega RC)^2} > 0, \quad \Im(Z) = - \frac{\omega R^2 C}{1 + (\omega RC)^2} < 0</math>となり、<br> | ||
RC並列回路の合成インピーダンス<math>\dot{Z}</math>のベクトルの向きは、必ず右下向き(複素数平面の第4象限)になる。<br> | RC並列回路の合成インピーダンス<math>\dot{Z}</math>のベクトルの向きは、必ず右下向き(複素数平面の第4象限)になる。<br> | ||
<br> | <br> | ||
| 82行目: | 234行目: | ||
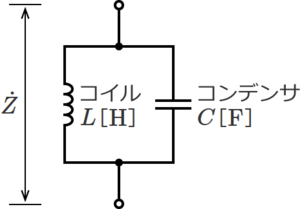
LC並列回路は、抵抗RとコンデンサCが並列に接続された回路で、下図のような回路になる。<br> | LC並列回路は、抵抗RとコンデンサCが並列に接続された回路で、下図のような回路になる。<br> | ||
[[ファイル:CircuitCalc Synthetic Impedance 3.png|フレームなし|中央]] | [[ファイル:CircuitCalc Synthetic Impedance 3.png|フレームなし|中央]] | ||
<center>図. | <center>図.7 コイルLとコンデンサCが並列接続の回路</center><br> | ||
<br> | <br> | ||
並列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、<br> | 並列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、<br> | ||
| 131行目: | 283行目: | ||
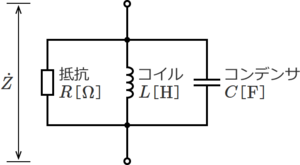
RLC並列回路は、抵抗R、コイルL、コンデンサCが並列に接続された回路で、下図のような回路になる。<br> | RLC並列回路は、抵抗R、コイルL、コンデンサCが並列に接続された回路で、下図のような回路になる。<br> | ||
[[ファイル:CircuitCalc Synthetic Impedance 4.png|フレームなし|中央]] | [[ファイル:CircuitCalc Synthetic Impedance 4.png|フレームなし|中央]] | ||
<center>図. | <center>図.8 抵抗R、コイルL、コンデンサCが並列接続の回路</center><br> | ||
<br> | <br> | ||
並列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、<br> | 並列回路の合成インピーダンス<math>\dot{Z}</math>を求める場合、<br> | ||
| 143行目: | 295行目: | ||
\begin{align} | \begin{align} | ||
\frac{1}{\dot{Z}} &= \dot{Y_1} + \dot{Y_2} + \dot{Y_3} = \frac{1}{R} + \frac{1}{j \omega L} + j \omega C \\ | \frac{1}{\dot{Z}} &= \dot{Y_1} + \dot{Y_2} + \dot{Y_3} = \frac{1}{R} + \frac{1}{j \omega L} + j \omega C \\ | ||
\dot{Z} &= \frac{1}{\dot{Y_1} + \dot{Y_2} + \dot{Y_3}} = \frac{j \omega RL}{R + j \omega L - \omega^2 RLC} \\ | \dot{Z} &= \frac{1}{\dot{Y_1} + \dot{Y_2} + \dot{Y_3}} = \frac{1}{\frac{1}{R} + \frac{1}{j \omega L} + j \omega C} \\ | ||
&= \frac{j \omega RL}{R + j \omega L - \omega^2 RLC} \\ | |||
&= \frac{j \omega RL}{R - \omega^2 RLC + j \omega L} \\ | &= \frac{j \omega RL}{R - \omega^2 RLC + j \omega L} \\ | ||
&= \frac{j \omega RL(R - \omega^2 RLC - j \omega L)}{(R - \omega^2 RLC)^2 + (\omega L)^2} \\ | &= \frac{j \omega RL(R - \omega^2 RLC - j \omega L)}{(R - \omega^2 RLC)^2 + (\omega L)^2} \\ | ||
| 152行目: | 305行目: | ||
</math><br> | </math><br> | ||
<br> | <br> | ||
<math>\omega \ge 0, \quad R > 0, \quad L > 0</math>であるため、<br> | <math>\omega \ge 0, \quad R > 0, \quad L > 0, \quad C > 0</math>であるため、<br> | ||
<math>\Re(Z) = \frac{\omega^2 R L^2}{R^2(1 - \omega^2 LC)^2 + (\omega L)^2} > 0, \quad -\infty < \Im(Z) = \frac{\omega R^2 L (1 - \omega^2 L C)}{R^2(1 - \omega^2 LC)^2 + (\omega L)^2} < \infty</math>となり、<br> | <math>\Re(Z) = \frac{\omega^2 R L^2}{R^2(1 - \omega^2 LC)^2 + (\omega L)^2} > 0, \quad -\infty < \Im(Z) = \frac{\omega R^2 L (1 - \omega^2 L C)}{R^2(1 - \omega^2 LC)^2 + (\omega L)^2} < \infty</math>となり、<br> | ||
RLC並列回路の合成インピーダンス<math>\dot{Z}</math>のベクトルの向きは、複素数平面の右上(第1象限)または右下(第4象限)または実数軸上となる。<br> | RLC並列回路の合成インピーダンス<math>\dot{Z}</math>のベクトルの向きは、複素数平面の右上(第1象限)または右下(第4象限)または実数軸上となる。<br> | ||
| 180行目: | 333行目: | ||
\end{align} | \end{align} | ||
</math><br> | </math><br> | ||
<br><br> | |||
== 例題 == | |||
==== 例題 1 ==== | |||
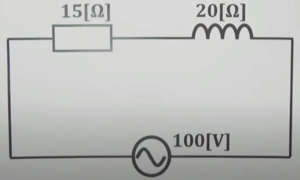
下図のようなRL回路がある時、抵抗に掛かる電圧を求める。<br> | |||
[[ファイル:CircuitCalc Synthetic Impedance 9.png|フレームなし|中央]] | |||
<br> | |||
回路のインピーダンス<math>\dot{Z}</math>とインピーダンスの大きさ<math>|Z|</math>は、次式となる。<br> | |||
<math>\dot{Z} = R + j \omega L = 15 + j20</math><br> | |||
<math>|Z| = \sqrt{15^2 + 20^2} = 25 \, [\Omega]</math><br> | |||
<br> | |||
全体に流れる電流Iの大きさ<math>|I|</math>は、次式となる。<br> | |||
<math>|I| = \frac{|V|}{|Z|} = \frac{100}{25} = 4 \, [ \mbox{A} ]</math><br> | |||
<br> | |||
したがって、抵抗に掛かる電圧<math>\dot{V_{R}}</math>は、次のようになる。<br> | |||
<math>\dot{V_{R}} = |I| \times R = 4 \times 15 = 60 \, [\mbox{V}]</math>となる。<br> | |||
<br> | |||
インダクタに掛かる電圧<math>\dot{V_{L}}</math>は、次のようになる。<br> | |||
<math>\dot{V_{L}} = |I| \times j \omega L = 4 \times j20 = j80 \, [\mbox{V}]</math>となる。<br> | |||
<br> | |||
電圧<math>\dot{V}</math>および電圧の大きさ<math>|V|</math>を求める場合は、次式のように計算する。<br> | |||
<math>\dot{V} = 60 + j80</math> より、<br> | |||
<math>|V| = \sqrt{60^2 + 80^2} = 100 \, [\mbox{V}]</math> となる。<br> | |||
<br> | |||
==== 例題 2 ==== | |||
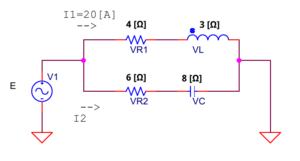
下図のような回路がある時、各抵抗、インダクタ、コンデンサに掛かる電圧を求める。<br> | |||
[[ファイル:CircuitCalc Synthetic Impedance 10.png|フレームなし|中央]] | |||
<br> | |||
電流I<sub>1</sub>より、<br> | |||
<math> | |||
\begin{align} | |||
\dot{V_{R1}} &= |I_1| \times R_1 = 20 \times 4 = 80 \, [\mbox{V}] \\ | |||
\dot{V_{L}} &= |I_1| \times j \omega L = 20 \times j3 = j60 \, [\mbox{V}] \\ | |||
|E| &= |V_1| = \sqrt{80^2 + 60^2} = 100 \, [\mbox{V}] | |||
\end{align} | |||
</math><br> | |||
<br> | |||
電流I<sub>2</sub>は、電源電圧100[V]と抵抗R<sub>2</sub>およびコンデンサCのインピーダンスZ<sub>2</sub>より、10[A]となる。<br> | |||
<math>|I_2| = \frac{|E|}{|Z_2|} = \frac{100}{\sqrt{6^2 + 8^2}} = 10 \, [\mbox{A}]</math><br> | |||
<br> | |||
回路に流れる全電流Iは、電源電圧Eから回路全体のインピーダンスZを除算することにより、求めることができる。<br> | |||
<math>\dot{Y_1} = \frac{1}{4 + j3}, \quad \dot{Y_2} = \frac{1}{6 - j8}</math><br> | |||
<math> | |||
\begin{align} | |||
\dot{Z} &= \frac{1}{\dot{Y}} \\ | |||
&= \frac{1}{\dot{Y_1} + \dot{Y_2}} \\ | |||
&= \frac{1}{\frac{1}{4 + j3} + \frac{1}{6 - j8}} = \frac{(4 + j3)(6 - j8)}{4 + j3 + 6 - j8} = \frac{48 - j14}{10 - j5} \\ | |||
&= \frac{(48 - j14)(10 + j5)}{125} = \frac{550 + j100}{125} = \frac{22 - j4}{5} \\ | |||
&= \frac{22}{5} - j \frac{4}{5} \\ | |||
\left | Z \right | &= \sqrt{\left ( \frac{22}{5} \right)^2 + \left ( \frac{4}{5} \right )^2} \\ | |||
& \cong 4.47 \, [\Omega] | |||
\end{align} | |||
</math><br> | |||
<br> | |||
<math>|I| = \frac{|E|}{|Z|} = \frac{100}{4.47} \cong 22.37 \, [\mbox{A}]</math> となる。<br> | |||
<br> | |||
または、次式のように求めることもできる。<br> | |||
<math>|I| = \sqrt{20^2 + 10^2} = 10 \sqrt{5} \, [\mbox{A}]</math><br> | |||
<br><br> | <br><br> | ||
__FORCETOC__ | __FORCETOC__ | ||
[[カテゴリ:回路計算]] | [[カテゴリ:回路計算]] | ||
2022年6月7日 (火) 00:00時点における最新版
概要
回路の受動素子(抵抗R、コイルL、コンデンサC)が直列接続または並列接続されている場合の合成インピーダンスの計算手順を記載する。
RL直列回路の合成インピーダンス
RL直列回路は、抵抗RとコイルLが直列に接続された回路で、下図のような回路になる。
直列回路の合成インピーダンスを求める場合、それぞれのインピーダンスを加算することにより求められる。
RL直列回路の合成インピーダンスは、次式で与えられる。
なお、角周波数である。
- 複素数表示の場合
であるため、となり、
RL直列回路の合成インピーダンスのベクトルの向きは、必ず右上向き(複素数平面の第1象限)になる。
- 合成インピーダンスの大きさの場合
RC直列回路の合成インピーダンス
RC直列回路は、抵抗RとコンデンサCが直列に接続された回路で、下図のような回路になる。
直列回路の合成インピーダンスを求める場合、それぞれのインピーダンスを加算することにより求められる。
RC直列回路の合成インピーダンスは、次式で与えられる。
なお、角周波数である。
- 複素数表示の場合
であるため、
となり、
RC直列回路の合成インピーダンスのベクトルの向きは、必ず右下向き(複素数平面の第4象限)になる。
- 合成インピーダンスの大きさの場合
LC直列回路の合成インピーダンス
LC直列回路は、抵抗RとコンデンサCが直列に接続された回路で、下図のような回路になる。
直列回路の合成インピーダンスを求める場合、それぞれのインピーダンスを加算することにより求められる。
LC直列回路の合成インピーダンスは、次式で与えられる。
なお、角周波数である。
- 複素数表示の場合
であるため、
となり、
LC直列回路の合成インピーダンスのベクトルの向きは、必ず、虚数軸上となる。
LC直列回路の合成インピーダンスは、上式の分母が正・負・ゼロの時、それぞれのベクトルの向きが変わる。
したがって、の時で、場合分けして考える必要がある。
- の場合
- 上式のリアクタンスが正になるため、合成インピーダンスのベクトルは、虚数軸上の正の向きになる。
- の場合
- 上式のリアクタンスが負になるため、合成インピーダンスのベクトルは、虚数軸上の負の向きになる。
- の場合
- 上式のリアクタンスが0になるため、合成インピーダンスのベクトルは、複素数平面の原点Oとなる。
- インピーダンスが0ということは、その回路は短絡状態と同じになる。
- また、 すなわち、 は、回路の共振条件である。
- 合成インピーダンスの大きさの場合
RLC直列回路の合成インピーダンス
RLC並列回路は、抵抗R、コイルL、コンデンサCが並列に接続された回路で、下図のような回路になる。
直列回路の合成インピーダンスを求める場合、それぞれのインピーダンスを加算することにより求められる。
RLC直列回路の合成インピーダンスは、次式で与えられる。
なお、角周波数である。
- 複素数表示の場合
であるため、
となり、
RLC直列回路の合成インピーダンスのベクトルの向きは、複素数平面の右上(第1象限)または右下(第4象限)または実数軸上となる。
RLC直列回路の合成インピーダンスは、上式の虚部()が正・負・ゼロの時、それぞれのベクトルの向きが変わる。
したがって、の時で、場合分けして考える必要がある。
- の場合
- 上式のリアクタンスが正になるため、合成インピーダンスのベクトルは、右上の向き(第1象限)になる。
- の場合
- 上式のリアクタンスが負になるため、合成インピーダンスのベクトルは、右下の向き(第4象限)になる。
- の場合
- 上式のリアクタンスが0になるため、合成インピーダンスのベクトルは、実数軸上の正の向きになる。()
- この条件を満たす周波数は共振周波数であるため、コイルLとコンデンサCの直列回路部分は短絡状態と同じになる。
- また、 すなわち、 は、回路の共振条件である。
- 合成インピーダンスの大きさの場合
RL並列回路の合成インピーダンス
RL並列回路は、抵抗RとコイルLが並列に接続された回路で、下図のような回路になる。
並列回路の合成インピーダンスを求める場合、
それぞれのインピーダンスの逆数(アドミタンス)を加算して、その逆数をとることにより求められる。
RL並列回路の合成インピーダンスは、次式で与えられる。
なお、角周波数である。
- 複素数表示の場合
であるため、
となり、
RL並列回路の合成インピーダンスのベクトルの向きは、必ず右上向き(複素数平面の第1象限)になる。
- 合成インピーダンスの大きさの場合
RC並列回路の合成インピーダンス
RC並列回路は、抵抗RとコンデンサCが並列に接続された回路で、下図のような回路になる。
並列回路の合成インピーダンスを求める場合、
それぞれのインピーダンスの逆数(アドミタンス)を加算して、その逆数をとることにより求められる。
RC並列回路の合成インピーダンスは、次式で与えられる。
なお、角周波数である。
- 複素数表示の場合
であるため、
となり、
RC並列回路の合成インピーダンスのベクトルの向きは、必ず右下向き(複素数平面の第4象限)になる。
- 合成インピーダンスの大きさの場合
LC並列回路の合成インピーダンス
LC並列回路は、抵抗RとコンデンサCが並列に接続された回路で、下図のような回路になる。
並列回路の合成インピーダンスを求める場合、
それぞれのインピーダンスの逆数(アドミタンス)を加算して、その逆数をとることにより求められる。
LC並列回路の合成インピーダンスは、次式で与えられる。
なお、角周波数である。
- 複素数表示の場合
であるため、
となり、
LC並列回路の合成インピーダンスのベクトルの向きは、必ず、虚数軸上となる。
LC並列回路の合成インピーダンスは、上式の分母が正・負・ゼロの時、それぞれのベクトルの向きが変わる。
したがって、の時で、場合分けして考える必要がある。
- の場合
- 上式のリアクタンスが正になるため、合成インピーダンスのベクトルは、虚数軸上の正の向きになる。
- の場合
- 上式のリアクタンスが負になるため、合成インピーダンスのベクトルは、虚数軸上の負の向きになる。
- の場合
- 上式のリアクタンスが無限大になるため、合成インピーダンスのベクトルは、虚数軸上の正の向きに無限大となる。
- インピーダンスが無限大ということは、その回路は開放状態と同じになる。
- また、 すなわち、 は、回路の共振条件である。
- 合成インピーダンスの大きさの場合
RLC並列回路の合成インピーダンス
RLC並列回路は、抵抗R、コイルL、コンデンサCが並列に接続された回路で、下図のような回路になる。
並列回路の合成インピーダンスを求める場合、
それぞれのインピーダンスの逆数(アドミタンス)を加算して、その逆数をとることにより求められる。
RLC並列回路の合成インピーダンスは、次式で与えられる。
なお、角周波数である。
- 複素数表示の場合
であるため、
となり、
RLC並列回路の合成インピーダンスのベクトルの向きは、複素数平面の右上(第1象限)または右下(第4象限)または実数軸上となる。
RLC並列回路の合成インピーダンスは、上式の分子(特に、)が正・負・ゼロの時、それぞれのベクトルの向きが変わる。
したがって、の時で、場合分けして考える必要がある。
- の場合
- 上式のリアクタンスが正になるため、合成インピーダンスのベクトルは、右上の向き(第1象限)になる。
- の場合
- 上式のリアクタンスが負になるため、合成インピーダンスのベクトルは、右下の向き(第4象限)になる。
- の場合
- 上式のリアクタンスが0になるため、合成インピーダンスのベクトルは、実数軸上の正の向きになる。()
- この条件を満たす周波数は反共振周波数であるため、コイルLとコンデンサCの並列回路部分は開放状態と同じになる。
- また、 すなわち、 は、回路の共振条件である。
- 合成インピーダンスの大きさの場合
例題
例題 1
下図のようなRL回路がある時、抵抗に掛かる電圧を求める。
回路のインピーダンスとインピーダンスの大きさは、次式となる。
全体に流れる電流Iの大きさは、次式となる。
したがって、抵抗に掛かる電圧は、次のようになる。
となる。
インダクタに掛かる電圧は、次のようになる。
となる。
電圧および電圧の大きさを求める場合は、次式のように計算する。
より、
となる。
例題 2
下図のような回路がある時、各抵抗、インダクタ、コンデンサに掛かる電圧を求める。
電流I1より、
電流I2は、電源電圧100[V]と抵抗R2およびコンデンサCのインピーダンスZ2より、10[A]となる。
回路に流れる全電流Iは、電源電圧Eから回路全体のインピーダンスZを除算することにより、求めることができる。
となる。
または、次式のように求めることもできる。


![{\displaystyle {\dot {Z}}=R+j\omega L\quad [\Omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0a49e27733cd081291f9ed432f4239b94ecc1aa)


![{\displaystyle {\begin{aligned}{\dot {Z}}&=R+j\omega L\\\left|Z\right|&={\sqrt {R^{2}+(\omega L)^{2}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/615d0beb3867597023ae2834be33da2d46b53e45)
![{\displaystyle {\begin{aligned}{\dot {Z}}&=R+{\frac {1}{j\omega C}}\\&=R-j{\frac {1}{\omega C}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72fef34e9ad25017b0b82506c416ee45d6492fc5)


![{\displaystyle {\begin{aligned}{\dot {Z}}&=R+{\frac {1}{j\omega C}}\\&=R-j{\frac {1}{\omega C}}\\\left|Z\right|&={\sqrt {R^{2}+\left({\frac {1}{\omega C}}\right)^{2}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d0e4c260f894d2244337d7298578fd2c1c41cbb)
![{\displaystyle {\begin{aligned}{\dot {Z}}&=j\omega L+{\frac {1}{j\omega C}}\\&=j\omega L-j{\frac {1}{\omega C}}\\&=j\left(\omega L-{\frac {1}{\omega C}}\right)\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bf319e3672dcbc2590963b0f8a2850a52b7fe4e)







![{\displaystyle {\begin{aligned}{\dot {Z}}&=j\omega L+{\frac {1}{j\omega C}}\\&=j\left(\omega L-{\frac {1}{\omega C}}\right)\\\left|Z\right|&={\sqrt {\left(\omega L-{\frac {1}{\omega C}}\right)^{2}}}\\&=\left|\omega L-{\frac {1}{\omega C}}\right|\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b1208e34c6484dfdb1656e20a01f729eb92becb)
![{\displaystyle {\begin{aligned}{\dot {Z}}&={\dot {Z_{1}}}+{\dot {Z_{2}}}+{\dot {Z_{3}}}=R+j\omega L+{\frac {1}{j\omega C}}\\&=R+j\omega L-j{\frac {1}{\omega C}}\\&=R+j(\omega L-{\frac {1}{\omega C}})\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58be2c4701954a25b8f39d91065db67a2d9a3f9b)




![{\displaystyle {\dot {Z}}=R[\Omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f459c60468d71f2d1003e8cab749412dff42c8f4)
![{\displaystyle {\begin{aligned}{\dot {Z}}&=R+j\omega L+{\frac {1}{j\omega C}}\\&=R+j(\omega L-{\frac {1}{\omega C}})\\\left|Z\right|&={\sqrt {R^{2}+\left(\omega L-{\frac {1}{\omega C}}\right)^{2}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80cd95ef3e83cf11baef8a3f4fe14c62692e8efa)
![{\displaystyle {\begin{aligned}{\frac {1}{\dot {Z}}}&={\dot {Y_{1}}}+{\dot {Y_{2}}}={\frac {1}{R}}+{\frac {1}{j\omega L}}\\{\dot {Z}}&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}}}={\frac {1}{{\frac {1}{R}}+{\frac {1}{j\omega L}}}}\\&={\frac {j\omega RL}{R+j\omega L}}\\&={\frac {j\omega RL(R-j\omega L)}{R^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}+j\omega R^{2}L}{R^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}}{R^{2}+(\omega L)^{2}}}+j{\frac {\omega R^{2}L}{R^{2}+(\omega L)^{2}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e7a1a4396d8eb22ec91358ddb184ef96df3cb49)

![{\displaystyle {\begin{aligned}{\dot {Z}}&={\frac {1}{{\frac {1}{R}}+{\frac {1}{j\omega L}}}}\\&={\frac {j\omega RL}{R+j\omega L}}\\\left|Z\right|&={\frac {\sqrt {(\omega RL)^{2}}}{\sqrt {R^{2}+(\omega L)^{2}}}}\\&={\frac {\omega RL}{\sqrt {R^{2}+(\omega L)^{2}}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee352af9cb301adf5905008e2c5a091182bc037c)
![{\displaystyle {\begin{aligned}{\frac {1}{\dot {Z}}}&={\dot {Y_{1}}}+{\dot {Y_{2}}}={\frac {1}{R}}+j\omega C\\{\dot {Z}}&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}}}={\frac {1}{{\frac {1}{R}}+j\omega C}}\\&={\frac {R}{1+j\omega RC}}\\&={\frac {R(1-j\omega RC)}{1+(\omega RC)^{2}}}\\&={\frac {R-j\omega R^{2}C}{1+(\omega RC)^{2}}}\\&={\frac {R}{1+(\omega RC)^{2}}}-j{\frac {\omega R^{2}C}{1+(\omega RC)^{2}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/109299c4e3ed67178752af5b92774563277a69c9)

![{\displaystyle {\begin{aligned}{\dot {Z}}&={\frac {1}{{\frac {1}{R}}+j\omega C}}\\&={\frac {R}{1+j\omega RC}}\\\left|Z\right|&={\frac {\sqrt {R^{2}}}{\sqrt {1^{2}+(\omega RC)^{2}}}}\\&={\frac {R}{\sqrt {1+(\omega RC)^{2}}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73d609efc49cc5b8220e8f83b00b821834e41af3)
![{\displaystyle {\begin{aligned}{\frac {1}{\dot {Z}}}&={\dot {Y_{1}}}+{\dot {Y_{2}}}={\frac {1}{j\omega L}}+j\omega C\\{\dot {Z}}&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}}}={\frac {1}{{\frac {1}{j\omega L}}+j\omega C}}\\&=j{\frac {\omega L}{1-\omega ^{2}LC}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d08719f56df71c06d365c7dddaba8029dc151336)




![{\displaystyle {\begin{aligned}{\dot {Z}}&={\frac {1}{{\frac {1}{j\omega L}}+j\omega C}}\\&={\frac {j\omega L}{1-\omega ^{2}LC}}\\\left|Z\right|&={\frac {\sqrt {(\omega L)^{2}}}{\sqrt {1^{2}+(\omega ^{2}LC)^{2}}}}\\&=\left|{\frac {\omega L}{\sqrt {1+(\omega ^{2}LC)^{2}}}}\right|\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3807c403f9dc21c03992b980065edbfe1c85591)
![{\displaystyle {\begin{aligned}{\frac {1}{\dot {Z}}}&={\dot {Y_{1}}}+{\dot {Y_{2}}}+{\dot {Y_{3}}}={\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C\\{\dot {Z}}&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}+{\dot {Y_{3}}}}}={\frac {1}{{\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C}}\\&={\frac {j\omega RL}{R+j\omega L-\omega ^{2}RLC}}\\&={\frac {j\omega RL}{R-\omega ^{2}RLC+j\omega L}}\\&={\frac {j\omega RL(R-\omega ^{2}RLC-j\omega L)}{(R-\omega ^{2}RLC)^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}+j\omega R^{2}L-j\omega ^{3}R^{2}L^{2}C}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}+j{\frac {\omega R^{2}L-\omega ^{3}R^{2}L^{2}C}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}\\&={\frac {\omega ^{2}RL^{2}}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}+j{\frac {\omega R^{2}L(1-\omega ^{2}LC)}{R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9e7a3740ed39432a71c37a06c39a4d476eff983)


![{\displaystyle {\begin{aligned}{\dot {Z}}&={\frac {j\omega RL}{R+j\omega L-\omega ^{2}RLC}}\\&={\frac {j\omega RL}{R-\omega ^{2}RLC+j\omega L}}\\&={\frac {j\omega RL}{R(1-\omega ^{2}LC)+j\omega L}}\\\left|Z\right|&={\frac {\sqrt {(\omega RL)^{2}}}{\sqrt {R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}}\\&={\frac {\omega RL}{\sqrt {R^{2}(1-\omega ^{2}LC)^{2}+(\omega L)^{2}}}}\quad [\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/217174d9664aefec8deaa3ff5b0c765e25c978e3)


![{\displaystyle |Z|={\sqrt {15^{2}+20^{2}}}=25\,[\Omega ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a87fad2965b320710c4cbb148fb3908ff1cb9917)

![{\displaystyle |I|={\frac {|V|}{|Z|}}={\frac {100}{25}}=4\,[{\mbox{A}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c6844b78b36efc774bcc243b6cf38d38685adc4)

![{\displaystyle {\dot {V_{R}}}=|I|\times R=4\times 15=60\,[{\mbox{V}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25d5f342e40c863dc776e08f9342cb1765c932f2)

![{\displaystyle {\dot {V_{L}}}=|I|\times j\omega L=4\times j20=j80\,[{\mbox{V}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2fccd678bc4567b3a0bbf2bcece5078b12151cb)



![{\displaystyle |V|={\sqrt {60^{2}+80^{2}}}=100\,[{\mbox{V}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad729e07aa42dc5f94b054c31591169c3d542201)
![{\displaystyle {\begin{aligned}{\dot {V_{R1}}}&=|I_{1}|\times R_{1}=20\times 4=80\,[{\mbox{V}}]\\{\dot {V_{L}}}&=|I_{1}|\times j\omega L=20\times j3=j60\,[{\mbox{V}}]\\|E|&=|V_{1}|={\sqrt {80^{2}+60^{2}}}=100\,[{\mbox{V}}]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/069b5b29fe81bffc523ea5370753f59e20c2c39d)
![{\displaystyle |I_{2}|={\frac {|E|}{|Z_{2}|}}={\frac {100}{\sqrt {6^{2}+8^{2}}}}=10\,[{\mbox{A}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02af54d0b989a3b12b5c68d3a323d47926e25798)

![{\displaystyle {\begin{aligned}{\dot {Z}}&={\frac {1}{\dot {Y}}}\\&={\frac {1}{{\dot {Y_{1}}}+{\dot {Y_{2}}}}}\\&={\frac {1}{{\frac {1}{4+j3}}+{\frac {1}{6-j8}}}}={\frac {(4+j3)(6-j8)}{4+j3+6-j8}}={\frac {48-j14}{10-j5}}\\&={\frac {(48-j14)(10+j5)}{125}}={\frac {550+j100}{125}}={\frac {22-j4}{5}}\\&={\frac {22}{5}}-j{\frac {4}{5}}\\\left|Z\right|&={\sqrt {\left({\frac {22}{5}}\right)^{2}+\left({\frac {4}{5}}\right)^{2}}}\\&\cong 4.47\,[\Omega ]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff7d89e1ee700311eea5f62b3731c9e584d2d30c)
![{\displaystyle |I|={\frac {|E|}{|Z|}}={\frac {100}{4.47}}\cong 22.37\,[{\mbox{A}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6e40838a263035fa9c0d21627ad70ba4da53a7c)
![{\displaystyle |I|={\sqrt {20^{2}+10^{2}}}=10{\sqrt {5}}\,[{\mbox{A}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf6f05e03a77b833f0451ff2b703ba90ddccd545)