「論理数学 - 写像」の版間の差分
ナビゲーションに移動
検索に移動
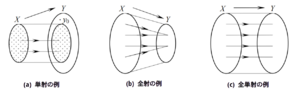
図(a). 単射の例
図(b). 単射でない例 図(a). 全射の例
図(b). 全射でない例 図(a). 単射の例
図(b). 全射の例
図(c). 全単射の例 図(a). 写像
図(b). 逆写像
(→単射) |
(→全単射) |
||
| 94行目: | 94行目: | ||
[[ファイル:Logical Mathematics Bijection 1.png|フレームなし|中央]] | [[ファイル:Logical Mathematics Bijection 1.png|フレームなし|中央]] | ||
<center>図(a). 単射の例<br>図(b). 全射の例<br>図(c). 全単射の例</center><br> | <center>図(a). 単射の例<br>図(b). 全射の例<br>図(c). 全単射の例</center><br> | ||
<br><br> | |||
== 逆写像 == | |||
定義 : | |||
集合Xから集合Yへの写像fが全単射である時、<math>\forall y \in Y</math> に対して、 | |||
<math>y = f(x)</math> を満たす要素 <math>x \in X</math> を対応させる写像をfの逆写像といい、<math>f^{-1}</math> で表す。 | |||
<math>y = f(x) \, \iff \, x = f^{-1}(y)</math> | |||
<br> | |||
<center>図(a). 写像<br>図(b). 逆写像</center><br> | |||
<br> | |||
例 : | |||
<math>f(x) = 2x + 1</math> の逆写像 <math>y = 2x + 1</math> とおき、xについて解く。 | |||
<math> | |||
\begin{array}{lcl} | |||
2x &=& y - 1 \\ | |||
x &=& \dfrac{1}{2} y - \dfrac{1}{2} | |||
\end{array} | |||
</math> | |||
したがって、 | |||
<math>f^{-1} (y) = \frac{1}{2} y - \frac{1}{2}</math> | |||
一般的に、写像はxの式で表すので、yをxに置き換えて次式のように表す。 | |||
<math>f^{-1} (x) = \frac{1}{2} y - \frac{1}{2}</math> | |||
<br><br> | <br><br> | ||
2024年4月30日 (火) 06:08時点における版
概要
写像 (関数) とは、ある集合Aの全ての要素に対して、集合Bの要素をただ1つ返すものである。
この時、集合Aを始域または定義域、集合Bを終域、関数の対応先となり得る集合𝐵の部分集合を値域という。
写像の定義
定義 : 集合Aの全ての要素に対して、その要素を入力すると集合Bの特定の要素をただ1つ出力するものを関数 (function) または 写像 (mapping) という。 この時、集合Aをその写像の始域または定義域 (domain) といい、集合Bを終域 (codomain) という。 また、集合Aを入力したときの出力となり得る集合Bの部分集合全体を関数 (写像) の値域 (像 range) という。
写像についての注意点を、以下に示す。
- 始域Aの全ての要素において、終域Bの要素をただ1つ返すこと。
- 始域Bの要素であれば、どの要素を返してもよい。
始域Aの各々の要素に対して、終域Bの同じ要素を返してもよい。
また、終域Bの全ての要素を対応付ける必要はない。 - 終域は、値域と呼ばれることもある。
恒等写像
定義 : 集合X上の写像 (定義域Xと終域Xが同一である写像) において、 に対して が成り立つ時、 を 上の恒等写像という。 補足 : は、集合Xの任意の要素aという意味である。
写像の表記
写像は関数 (function) の頭文字を用いて、と表記されることが多い。
2つ以上の写像がある場合は、アルファベット順に 等と表記する。
始域が集合A、終域が集合Bである写像 を、 と記述する。
集合Aの各要素 に対して、それに対応する集合Bの要素が であるとき、これを または と記述する。
また,終域・値域は、 と記述する。
写像の例
は実数全体の集合、 は整数全体の集合を表す。
例題 1: があるとする。 この写像は、英語の小文字を入力する時、その大文字を出力する。 この時、 であり、終域・値域は である。
例題 2: があるとする。 この写像は、整数を入力する時、2で剰余した値を出力する。 この時、 であり、値域は である。
例題 3: があるとする。 この写像は、 と定義する。 この時、 であり、値域は である。
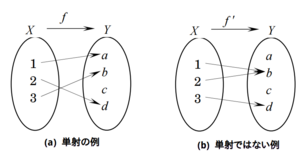
単射
定義 : 始域Xから終域Yへの写像fが に対して、常に を満たす時、 写像fは単射 (1対1対応) であるという。 補足 : 対偶 に対して、常に を満たす、と同義である。
図(b). 単射でない例
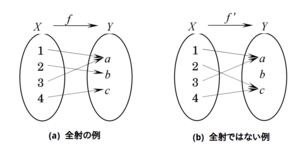
全射
定義 : 始域Xから終域Yへの写像fについて、 に対して、常に を満たす要素 が存在する時、 写像fは全射(上への対応)であるという。
図(b). 全射でない例
全単射
定義 : 全射であり、かつ、単射である写像を全単射 (上への1対1対応) という。
図(b). 全射の例
図(c). 全単射の例
逆写像
定義 : 集合Xから集合Yへの写像fが全単射である時、 に対して、 を満たす要素 を対応させる写像をfの逆写像といい、 で表す。
図(b). 逆写像
例 : の逆写像 とおき、xについて解く。 したがって、 一般的に、写像はxの式で表すので、yをxに置き換えて次式のように表す。