第3回 - 2変数間の相関

概要

記述統計において、2変数間の相関を表すために、次の事項を学習する。

1. 散布図と相関関係
2. 2変数間の相関 - 相関係数で定量化
3. 2変数間の相関の注意点

散布図と相関関係

2変数xとyの組(x, y)について、横軸にx、縦軸にyを取り、データ点としてプロットしたものを散布図という。

散布図上の点の分布が「直線関係」に近い傾向があるとき、「相関関係がある」という。

散布図で相関関係があるとき、2変数xとyの間には、何らかの関係があると考えられる。
今までは散布図を見て、感覚的にxとyの間に関係があると考えてきたが、記述統計学では、相関関係を定量的に取り扱うことができる。

2変数間の相関

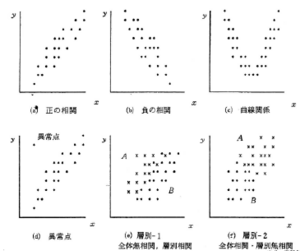
2変数を並べたデータについて、横軸を変数X、縦軸を変数Yとして散布図を書くと、

• Xが増加するとYも増加する場合

  正の相関

• Xが増加するとYが減少する場合

  負の相関

• Xが増加してもYに影響が無い場合

  無相関(当てはめた直線の傾き=0も含む)

2変数間の相関について数値化できる。 ⇒ 相関係数で表現できる。

• 共分散

  $C_{xy}={\frac {1}{n}}\sum _{i=1}^{N}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})$

• 各変数の母分散

  $\sigma _{x}^{2}={\frac {1}{n}}\sum _{i=1}^{N}(x_{i}-{\bar {x}})^{2}$

  $\sigma _{y}^{2}={\frac {1}{n}}\sum _{i=1}^{N}(y_{i}-{\bar {y}})^{2}$

• 相関係数(ピアソンの積率相関係数)

  $r_{xy}={\frac {C_{xy}}{{\sqrt {\sigma _{x}^{2}}}{\sqrt {\sigma _{y}^{2}}}}}$

  $-1\leq r_{xy}\leq 1$

相関係数は、2変数が直線に乗る程度を表す。絶対値が1に近いほど、2変数間の相関が強い。
$r_{xy}=1$ : 正の完全相関
データ点が正の傾きの直線上に乗る。

$r_{xy}=-1$ : 負の完全相関
データ点が負の傾きの直線上に乗る。

2変数の相関係数を計算するだけでは不十分である。必ず散布図を書いて、実際に目で見てみることが重要である。

• 相関係数の値と散布図

  相関係数の値が大きくとも、データ点数が少ないと目で見た場合に相関がなさそうな場合がある。

  

• 同じ相関係数の値を示す異なる散布図

  

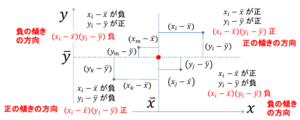
共分散の意味

2変数の両平均値の点$({\bar {x}},{\bar {y}})$から見て、各データ点$(x_{i},y_{i})$が、正の傾きの方向または負の傾きの方向に偏っているかを$(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})$で計算した後、
全データ点の傾向を$(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})$の平均値で表しているといえる。

データの標準化

データの平均x、標準偏差s_xであるとき、データを加工して、平均を0、標準偏差を1に変換することを標準化という。

元のデータx_iを標準化したデータu_iにするには、以下のように変換する。
$u_{i}={\frac {(x_{i}-{\bar {x}})}{s_{x}}}$
${\mbox{標 準 化 デ ー タ }}={\frac {({\mbox{元 デ ー タ }}-{\mbox{平 均 }})}{\mbox{標 準 偏 差 }}}$

相関係数の計算で、2変数(x, y)を標準化(平均を0、標準偏差を1)したものの共分散を計算すると、それが相関係数になる。

• 変数xとyの標準化

  $u_{xi}={\frac {(x_{i}-{\bar {x}})}{s_{x}}}$

  $u_{yi}={\frac {(y_{i}-{\bar {y}})}{s_{y}}}$
  

  
  

• 標準化したxとyの共分散を計算すると、相関係数に等しい。

  $C_{uxuy}={\frac {1}{n-1}}\sum _{i=1}^{N}(u_{xi}-{\bar {u}}_{x})(u_{yi}-{\bar {u}}_{y})$

  $={\frac {1}{n-1}}\sum _{i=1}^{N}u_{xi}u_{yi}$

  $={\frac {1}{n-1}}\sum _{i=1}^{N}{\frac {(x_{i}-{\bar {x}})}{s_{x}}}{\frac {(y_{i}-{\bar {y}})}{s_{y}}}$

  $={\frac {{\frac {1}{n-1}}\sum _{i=1}^{N}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{{\sqrt {V_{x}}}{\sqrt {V_{y}}}}}$

  $=r_{xy}$

2変数間の相関での注意点

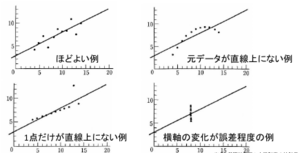
2変数の相関を検討するときは、必ず散布図を書くこと。 散布図のチェックポイントは以下の通りである。

1. 2次元正規分布と見なせるか？
2. 相関関係は、正か負か？
3. 直線関係か? 曲線関係か？
4. 異常な点(外れ値)はないか？
5. 層別する必要はないか？(層別は、異なるグループを分けて散布図を書くこと)

例題 : 相関分析

ある5人の身長と体重のデータについて、相関分析を行なう。

身長(cm)	体重(kg)
150.2	56.4
155.0	52.9
163.5	72.2
172.1	68.1
178.6	79.7

• 身長の平均

  163.9 [cm]

• 体重の平均

  65.9 [kg]

• 身長の母分散

  110.1 [cm²]

• 体重の母分散

  99.3 [kg²]

• 身長の母標準偏差

  ${\sqrt {110.1}}=10.5{\mbox{[cm]}}$

• 体重の母標準偏差

  ${\sqrt {99.3}}=10.0{\mbox{[kg]}}$

• 身長と体重の共分散

  93.1 [cm・kg]

• 相関係数

  $r_{xy}={\frac {93.1}{10.5\times 10.0}}=0.890$