「回路計算 - スターデルタ変換」の版間の差分
(→概要) |
(→電圧の大きさ) |
||
| (同じ利用者による、間の5版が非表示) | |||
| 11行目: | 11行目: | ||
<u>デルタ結線では、相電流は線電流の <math>\frac{1}{\sqrt{3}}</math> となる。</u><br> | <u>デルタ結線では、相電流は線電流の <math>\frac{1}{\sqrt{3}}</math> となる。</u><br> | ||
主に、変圧器の高圧側や大型の誘導電動機で使用されることが多く、大電流に適している。<br> | 主に、変圧器の高圧側や大型の誘導電動機で使用されることが多く、大電流に適している。<br> | ||
<br> | |||
[[ファイル:Star-Delta 1.png|フレームなし|中央]] | |||
<br> | <br> | ||
これら2つの結線方式の主な特徴を比較する。<br> | これら2つの結線方式の主な特徴を比較する。<br> | ||
| 29行目: | 31行目: | ||
<br> | <br> | ||
これらの結線方式は、電気設備の設計や保守において非常に重要な基礎知識となる。<br> | これらの結線方式は、電気設備の設計や保守において非常に重要な基礎知識となる。<br> | ||
<br><br> | |||
== 相電圧と線間電圧 == | |||
これらの電圧関係は、三相交流回路の解析や設計において非常に重要である。<br> | |||
<br> | |||
特に、変圧器やモータ等の機器の結線方式を選択する場合の基準となる。<br> | |||
<br> | |||
==== スター結線 (Y結線) の場合 ==== | |||
* 相電圧 | |||
*: 中性点 (N) と各相端子 (A、B、C) 間の電圧を指す。 | |||
*: 下図の青い矢印で示している。 | |||
<br> | |||
* 線間電圧 | |||
*: 各相端子間 (A-B間、B-C間、C-A間) の電圧を指す。 | |||
*: 下図の赤い矢印で示している。 | |||
*: 線間電圧は、相電圧の <math>\sqrt{3}</math> 倍となる。 | |||
<br> | |||
==== デルタ結線 (Δ結線) の場合 ==== | |||
* 相電圧 | |||
*: 各辺 (抵抗やコイル) に加わる電圧を指す。 | |||
*: 下図の青い矢印で示している。 | |||
<br> | |||
* 線間電圧 | |||
*: 各端子間 (A-B間、B-C間、C-A間) の電圧を指す。 | |||
*: 下図の赤い矢印で示している。 | |||
*: 相電圧と線間電圧は等しくなる。 | |||
<br><br> | |||
== Y結線における線間電圧と相電圧の関係 == | |||
==== 電圧の大きさ ==== | |||
Y結線における線間電圧が相電圧の <math>\sqrt{3}</math> 倍になる理由は、三相交流のベクトル関係から説明できる。<br> | |||
<br> | |||
三相交流における各相電圧は、時間的に120度ずつ位相がずれている。<br> | |||
下図において、黒い矢印は各相電圧ベクトル (E<sub>U</sub>、E<sub>V</sub>、E<sub>W</sub>)、青い矢印は線間電圧ベクトル (E<sub>UV</sub>) とする。<br> | |||
<br> | |||
[[ファイル:Star-Delta 3.png|フレームなし|中央]] | |||
<br> | |||
線間電圧が相電圧の <math>\sqrt{3}</math> 倍になる計算過程を以下に示す。<br> | |||
<br> | |||
各相電圧ベクトルは大きさが等しく (Eとおく) 、互いに120度の角度をなす。<br> | |||
線間電圧は2つの相電圧ベクトルの差として表される。<br> | |||
<br> | |||
例えば、U相とV相間の線間電圧E<sub>UV</sub>は、<math>E_{UV} = E_U - E_V</math> である。<br> | |||
<br> | |||
2つのベクトルのなす角が120°の場合、その差ベクトルの大きさは<u>余弦定理</u>より次式で求められる。<br> | |||
<math>|E_{UV}| = \sqrt{(E_U)^2 + (E_V)^2 - 2 \cdot E_U \cdot E_V \cdot \cos{120^\circ}}</math><br> | |||
<br> | |||
<math>\cos{120^\circ} = -0.5</math> なので、<br> | |||
<math> | |||
\begin{align} | |||
|E_{UV}| &= \sqrt{E^2 + E^2 - 2 \cdot E \cdot E \cdot (-0.5)} \\ | |||
&= \sqrt{2E^2 + E^2} \\ | |||
&= \sqrt{3}E | |||
\end{align} | |||
</math><br> | |||
<br> | |||
上記のように、ベクトルの演算により、線間電圧は相電圧の<math>\sqrt{3}</math> 倍となることが証明される。 | |||
<br> | |||
これは、三相交流システムの重要な特性の1つであり、変圧器やモータの設計、電力供給システムの構築において基本的な関係である。<br> | |||
<br> | |||
==== 位相 ==== | |||
Y結線の三相交流回路では、線間電圧の位相が相電圧よりも30°進む。<br> | |||
<br> | |||
まず、u相とv相に着目すると、相電圧E<sub>U</sub>と相電圧E<sub>V</sub>は位相が120°ずれるため、ベクトルで表すと下図(a)のようになる。<br> | |||
ここで、線間電圧V<sub>UV</sub>は、E<sub>U</sub>と-E<sub>V</sub>を足したものである。<br> | |||
<br> | |||
V<sub>UV</sub>の大きさは下図(b)のような直角三角形が現れることから、EUの <math>\sqrt3</math> 倍となり、位相がE<sub>U</sub>に比べて30°進むことが理解できる。<br> | |||
<br> | |||
[[ファイル:Star-Delta 4.png|フレームなし|中央]] | |||
<br><br> | |||
== Δ結線における線間電圧と相電圧の関係 == | |||
==== 電圧の大きさ ==== | |||
Δ結線における線間電圧と相電圧が同じになる。<br> | |||
<br> | |||
Δ結線の構造的特徴<br> | |||
* 3つの巻線が三角形状に接続されている。 | |||
* 各巻線の端子が直接負荷に接続されている。 | |||
* 巻線間に他の経路がない。 | |||
<br> | |||
電気的な観点<br> | |||
* 相電圧 | |||
*: 各巻線にかかる電圧 (V<sub>PH</sub>) | |||
* 線間電圧 | |||
*: 線と線の間の電圧 (V<sub>L</sub>) | |||
* Δ結線では、負荷端子は巻線の端子と直接接続されている。 | |||
<br> | |||
そのため、線間電圧を測定する場合、測定点は巻線の両端と同じ位置になる。<br> | |||
したがって、<math>V_L = V_{PH}</math> となる。<br> | |||
<br> | |||
これはY結線と大きく異なる点である。<br> | |||
Y結線の場合は、<math>\mbox{ 線 間 電 圧 } \, = \mbox{ 相 電 圧 } \times \sqrt{3}</math> となるが、Δ結線ではそのような変換は発生しない。<br> | |||
<br> | |||
このシンプルな関係は、Δ結線の大きな特徴の1つである。<br> | |||
機器の設計や電圧管理において、この特性を活かすことができる。<br> | |||
<br> | |||
==== 位相 ==== | |||
Δ結線における線間電圧と相電圧の位相が同じになる。<br> | |||
<br> | |||
Δ結線の構造的特徴<br> | |||
* 3つの巻線 (相巻線) が、a-b-c-aのように三角形状に接続されている。 | |||
* 各頂点から外部端子 (R-S-T) が引き出されている。 | |||
* 各相巻線の端子が直接外部端子に接続される。 | |||
<br> | |||
電圧の定義<br> | |||
* 相電圧 | |||
*: 各巻線にかかる電圧 | |||
*: 例: Vab, Vbc, Vca | |||
* 線間電圧 | |||
*: 外部端子間の電圧 | |||
*: 例: VRS, VST, VTR | |||
<br> | |||
位相が同じになる理由として、相電圧Vabと線間電圧VRSの例で考えると、<br> | |||
* Vabは巻線a-b間の電圧 | |||
* VRSは端子R-S間の電圧 | |||
* 端子RはaにつながっているR | |||
* 端子SはbにつながっているS | |||
* したがって、VRSはVabと全く同じ電圧を測定することになる | |||
<br> | |||
重要な点として、<br> | |||
* Δ結線では測定点が巻線端子と同じ位置 | |||
* 巻線間に他の経路が存在しない | |||
* 直接的な接続により、電圧の変換や位相のずれが生じない | |||
<br> | |||
これにより、Δ結線では線間電圧と相電圧は、大きさと位相が同じとなる。<br> | |||
<br><br> | <br><br> | ||
| 39行目: | 166行目: | ||
==== 抵抗値の変換 ==== | ==== 抵抗値の変換 ==== | ||
スター結線の抵抗をR<sub>A</sub>、R<sub>B</sub>、R<sub>C</sub>、変換後のデルタ結線の抵抗をR<sub>AB</sub>、R<sub>BC</sub>、R<sub>CA</sub>とする時、次式で求められる。<br> | スター結線の抵抗をR<sub>A</sub>、R<sub>B</sub>、R<sub>C</sub>、変換後のデルタ結線の抵抗をR<sub>AB</sub>、R<sub>BC</sub>、R<sub>CA</sub>とする時、次式で求められる。<br> | ||
<br> | |||
[[ファイル:Star-Delta 2.png|フレームなし|中央]] | |||
<br> | <br> | ||
<math> | <math> | ||
2024年11月10日 (日) 02:40時点における最新版
概要
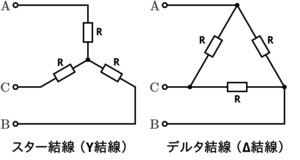
スター結線 (Y結線) は、3つの巻線の一端を共通の中性点 (ニュートラルポイント) で接続する方式である。
形状が「Y」の文字に似ていることから、Y結線とも呼ばれている。
スター結線では、各相の電圧 (相電圧) は線間電圧の となる。
主に、変圧器の低圧側や誘導電動機の固定子巻線で使用されており、家庭用電源としても広く採用されている。
デルタ結線 (Δ結線) は、3つの巻線を三角形状に接続する方式である。
ギリシャ文字のΔ (デルタ) に形状が似ていることから、この名称がついている。
デルタ結線では、相電流は線電流の となる。
主に、変圧器の高圧側や大型の誘導電動機で使用されることが多く、大電流に適している。
これら2つの結線方式の主な特徴を比較する。
- スター結線
- 中性点があるため、単相負荷にも対応可能
- 絶縁耐力の面で有利
- 小電流向き
- デルタ結線
- 大電流に適している
- 相間の電圧と線間の電圧が等しい
- 故障時でも運転継続が可能な場合がある
実際の使用場面では、これらの特徴を考慮して使い分けられる。
例えば、配電系統では需要家側 (低圧側) にスター結線を、送電側 (高圧側) にデルタ結線を採用することが一般的である。
また、変圧器では1次側と2次側で異なる結線方式を組み合わせることにより、位相差の調整なども行っている。
これらの結線方式は、電気設備の設計や保守において非常に重要な基礎知識となる。
相電圧と線間電圧
これらの電圧関係は、三相交流回路の解析や設計において非常に重要である。
特に、変圧器やモータ等の機器の結線方式を選択する場合の基準となる。
スター結線 (Y結線) の場合
- 相電圧
- 中性点 (N) と各相端子 (A、B、C) 間の電圧を指す。
- 下図の青い矢印で示している。
- 線間電圧
- 各相端子間 (A-B間、B-C間、C-A間) の電圧を指す。
- 下図の赤い矢印で示している。
- 線間電圧は、相電圧の 倍となる。
デルタ結線 (Δ結線) の場合
- 相電圧
- 各辺 (抵抗やコイル) に加わる電圧を指す。
- 下図の青い矢印で示している。
- 線間電圧
- 各端子間 (A-B間、B-C間、C-A間) の電圧を指す。
- 下図の赤い矢印で示している。
- 相電圧と線間電圧は等しくなる。
Y結線における線間電圧と相電圧の関係
電圧の大きさ
Y結線における線間電圧が相電圧の 倍になる理由は、三相交流のベクトル関係から説明できる。
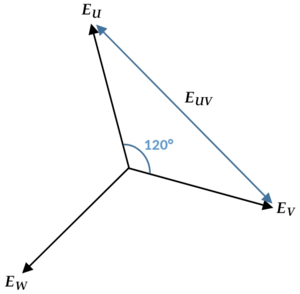
三相交流における各相電圧は、時間的に120度ずつ位相がずれている。
下図において、黒い矢印は各相電圧ベクトル (EU、EV、EW)、青い矢印は線間電圧ベクトル (EUV) とする。
線間電圧が相電圧の 倍になる計算過程を以下に示す。
各相電圧ベクトルは大きさが等しく (Eとおく) 、互いに120度の角度をなす。
線間電圧は2つの相電圧ベクトルの差として表される。
例えば、U相とV相間の線間電圧EUVは、 である。
2つのベクトルのなす角が120°の場合、その差ベクトルの大きさは余弦定理より次式で求められる。
なので、
上記のように、ベクトルの演算により、線間電圧は相電圧の 倍となることが証明される。
これは、三相交流システムの重要な特性の1つであり、変圧器やモータの設計、電力供給システムの構築において基本的な関係である。
位相
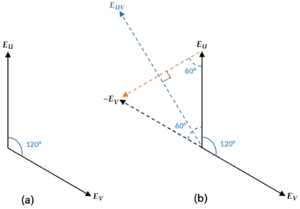
Y結線の三相交流回路では、線間電圧の位相が相電圧よりも30°進む。
まず、u相とv相に着目すると、相電圧EUと相電圧EVは位相が120°ずれるため、ベクトルで表すと下図(a)のようになる。
ここで、線間電圧VUVは、EUと-EVを足したものである。
VUVの大きさは下図(b)のような直角三角形が現れることから、EUの 倍となり、位相がEUに比べて30°進むことが理解できる。
Δ結線における線間電圧と相電圧の関係
電圧の大きさ
Δ結線における線間電圧と相電圧が同じになる。
Δ結線の構造的特徴
- 3つの巻線が三角形状に接続されている。
- 各巻線の端子が直接負荷に接続されている。
- 巻線間に他の経路がない。
電気的な観点
- 相電圧
- 各巻線にかかる電圧 (VPH)
- 線間電圧
- 線と線の間の電圧 (VL)
- Δ結線では、負荷端子は巻線の端子と直接接続されている。
そのため、線間電圧を測定する場合、測定点は巻線の両端と同じ位置になる。
したがって、 となる。
これはY結線と大きく異なる点である。
Y結線の場合は、 となるが、Δ結線ではそのような変換は発生しない。
このシンプルな関係は、Δ結線の大きな特徴の1つである。
機器の設計や電圧管理において、この特性を活かすことができる。
位相
Δ結線における線間電圧と相電圧の位相が同じになる。
Δ結線の構造的特徴
- 3つの巻線 (相巻線) が、a-b-c-aのように三角形状に接続されている。
- 各頂点から外部端子 (R-S-T) が引き出されている。
- 各相巻線の端子が直接外部端子に接続される。
電圧の定義
- 相電圧
- 各巻線にかかる電圧
- 例: Vab, Vbc, Vca
- 線間電圧
- 外部端子間の電圧
- 例: VRS, VST, VTR
位相が同じになる理由として、相電圧Vabと線間電圧VRSの例で考えると、
- Vabは巻線a-b間の電圧
- VRSは端子R-S間の電圧
- 端子RはaにつながっているR
- 端子SはbにつながっているS
- したがって、VRSはVabと全く同じ電圧を測定することになる
重要な点として、
- Δ結線では測定点が巻線端子と同じ位置
- 巻線間に他の経路が存在しない
- 直接的な接続により、電圧の変換や位相のずれが生じない
これにより、Δ結線では線間電圧と相電圧は、大きさと位相が同じとなる。
Y-Δ変換 (スターデルタ変換)
スター結線 (Y結線) とデルタ結線 (Δ結線) は、互いに等価な回路に変換することができる。
スター結線 (Y結線) を等価なデルタ結線 (Δ結線) に変換する時、この変換をスターデルタ変換という。
スターデルタ変換は、スターデルタ等価変換と呼ばれることもある。
抵抗値の変換
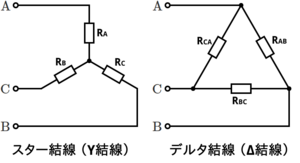
スター結線の抵抗をRA、RB、RC、変換後のデルタ結線の抵抗をRAB、RBC、RCAとする時、次式で求められる。
上式は、分子が3つの抵抗値の積の組み合わせの和となっており、分母がその対角に位置する抵抗値となっていることが特徴である。
分子部分をZとおいて、 とする時、次式のように表すこともできる。
次式のように整理する場合、計算がより簡単になる。
この変換式を使用することにより、スター結線の回路を等価なデルタ結線の回路に変換することができる。
なお、3つの抵抗が同じ場合は、 となり、
となるため、スターデルタ変換後のデルタ結線 (Δ結線) の抵抗値は、スター結線 (Y結線) の抵抗値の3倍になる。