統計学 - 連続型確率分布

確率密度

離散型でのサンプル数を増加させて、各区間の幅を減少させた時のヒストグラムの極限 (幅を0に近付ける) が連続型での確率密度の曲線になる。
連続型での確率密度の値は、離散型でのヒストグラムの縦軸の値に相当する。

離散型での確率関数Piの代わりに、連続型では確率密度 $f(x)$ を用いる。

連続型での確率密度 $f(x)$ は、$\int _{a}^{b}f(x)\,dx$ と積分することにより確率となる。

確率密度 $f(x)$ 単体は、各xの値の発生確率に比例する相対値の意味である。

例えば、サイコロの目が $X=1,2,3,4,5,6$ ではなく、0～6の間の実数値とする場合、0～6の間の実数は無限個 (全体集合の個数 $n(U)=\infty$ ) となる。
つまり、0～6の間の実数Xを1つ取る時、その確率は、${\dfrac {1}{n(U)}}={\dfrac {1}{\infty }}=0$ となる。
連続型では、ある実数1つを取る確率は0となる。

しかし、$1\leq x\leq 3$ の実数の範囲とする時、その確率は、${\dfrac {1\leq x\leq 3}{0\leq x\leq 6}}={\dfrac {1}{3}}$ となる。

連続型では、離散型での確率関数Piで確率が計算できない。(実数1つの確率が連続型では必ず0のため)

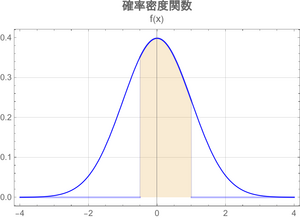
連続型では、次式のように、実数の範囲の確率を積分で考える。
つまり、確率密度関数f(x)の面積で確率を考える。
$P(a\leq x\leq b)=\int _{a}^{b}f(x)\,dx$

• 離散型では全確率関数の和 (= 1)

  $\sum _{i=1}^{n}P_{i}=1$

• 連続型では実数の全範囲の積分 (= 1)

  $P(-\infty \leq x\leq \infty )=\int _{-\infty }^{\infty }f(x)\,dx=1$

累積分布関数

• 離散型での累積分布関数

  xより小さい確率変数の実現値xiに対応する確率関数Piの和

  $F(x)=\sum _{x_{i}\leq x}P_{i}$

• 連続型での累積分布関数

  $F(x)=\int _{-\infty }^{x}f(t)\,dt$

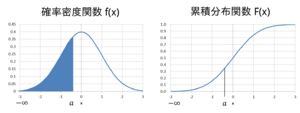
累積分布関数のグラフ

連続型での累積分布関数
$F(a)=\int _{-\infty }^{a}f(t)\,dt$

累積分布関数の性質

累積分布関数F(x)は、単調に増加する。
$a\leq b$ ならば、$F(a)\leq F(b)$

$F(\infty )=0,\quad F(\infty )=1$

${\begin{aligned}P(a\leq x\leq b)&=\int _{a}^{b}f(x)\,dx\\&=\int _{-\infty }^{b}f(x)\,dx-\int _{-\infty }^{a}f(x)\,dx\\&=F(b)-F(a)\end{aligned}}$

連続型確率分布の期待値

• 離散型での期待値

  $\mu =E[X]=\sum _{i=1}{n}x_{i}\cdot P_{i}=x_{1}P_{1}+x_{2}P_{2}+\cdots +x_{n}P_{n}$

• 連続型での期待値

  $\mu =E[X]=\int _{-\infty }^{\infty }x\cdot f(x)\,dx$

連続型確率分布の分散

• 離散型での分散

  $\sigma ^{2}=V[X]=\sum _{i=1}^{n}(x_{i}-\mu )^{2}\cdot P_{i}=(x_{1}-\mu )^{2}\cdot P_{1}+(x_{2}-\mu )^{2}\cdot P_{2}+\cdots +(x_{n}-\mu )^{2}\cdot P_{n}$

• 連続型での分散

  $\sigma ^{2}=V[X]=\int _{-\infty }^{\infty }(x-\mu )^{2}\cdot f(x)\,dx=E[X^{2}]-E[X]\cdot E[X]$

離散型確率分布および連続型確率分布の両方において、標準偏差σは $\sigma ={\sqrt {V[X]}}$ である。