「統計学 - モンティホール問題」の版間の差分
(ページの作成:「== 概要 == モンティホール問題とは、確率論のパラドックスとして広く知られている問題である。<br> これは、アメリカのテレビ番組Let's Make a Dealの司会者だったモンティ・ホールにちなんで名付けられた。<br> <br> # プレイヤーの前には3つのドアが用意されており、そのうちの1つのドアの後ろには高価な車、残りの2つのドアの後ろにはヤギが置かれて…」) |
(→概要) |
||
| 7行目: | 7行目: | ||
# その後、司会者のモンティは、プレイヤーが選んでいないドアの中から、必ずヤギがいるドアを1つ開けて見せる。 | # その後、司会者のモンティは、プレイヤーが選んでいないドアの中から、必ずヤギがいるドアを1つ開けて見せる。 | ||
# 最後に、プレイヤーは最初に選んだドアをそのままにするか、もう1つの閉じたドアに選択を変更するかを決めることができる。 | # 最後に、プレイヤーは最初に選んだドアをそのままにするか、もう1つの閉じたドアに選択を変更するかを決めることができる。 | ||
<br> | |||
[[ファイル:Monty Hall Problem 1.png|中央]] | |||
<br> | |||
[[ファイル:Monty Hall Problem 2.png|中央]] | |||
<br> | <br> | ||
この問題の核心は、プレイヤーはドアを変更すべきかどうかという点にある。<br> | この問題の核心は、プレイヤーはドアを変更すべきかどうかという点にある。<br> | ||
| 15行目: | 19行目: | ||
これは、最初の選択時の確率がそのまま維持されるためである。<br> | これは、最初の選択時の確率がそのまま維持されるためである。<br> | ||
一方で、ドアを変更した場合の当たる確率は <math>\dfrac{2}{3}</math> となる。<br> | 一方で、ドアを変更した場合の当たる確率は <math>\dfrac{2}{3}</math> となる。<br> | ||
<br> | |||
[[ファイル:Monty Hall Problem 3.png|中央]] | |||
<br> | <br> | ||
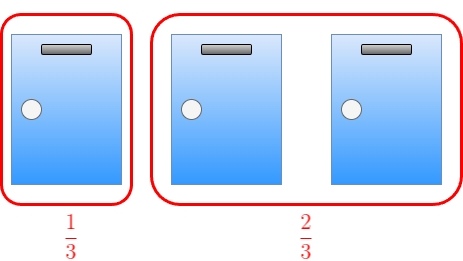
これは、最初の選択時において、プレイヤーが正解のドアを選ぶ確率は <math>\dfrac{1}{3}</math>、ハズレのドアを選ぶ確率は <math>\dfrac{2}{3}</math> である。<br> | これは、最初の選択時において、プレイヤーが正解のドアを選ぶ確率は <math>\dfrac{1}{3}</math>、ハズレのドアを選ぶ確率は <math>\dfrac{2}{3}</math> である。<br> | ||
2025年1月5日 (日) 21:39時点における版
概要
モンティホール問題とは、確率論のパラドックスとして広く知られている問題である。
これは、アメリカのテレビ番組Let's Make a Dealの司会者だったモンティ・ホールにちなんで名付けられた。
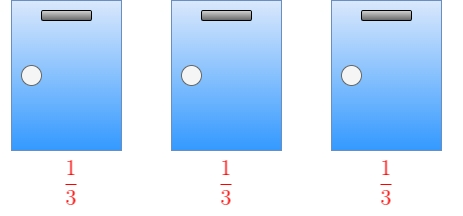
- プレイヤーの前には3つのドアが用意されており、そのうちの1つのドアの後ろには高価な車、残りの2つのドアの後ろにはヤギが置かれている。
- プレイヤーは最初に1つのドアを選択する。
- その後、司会者のモンティは、プレイヤーが選んでいないドアの中から、必ずヤギがいるドアを1つ開けて見せる。
- 最後に、プレイヤーは最初に選んだドアをそのままにするか、もう1つの閉じたドアに選択を変更するかを決めることができる。
この問題の核心は、プレイヤーはドアを変更すべきかどうかという点にある。
直感的には、残された2つのドアのどちらかを選ぶため、確率は になると考えがちである。
しかし、実際の確率は大きく異なる。
もし、最初の選択をそのままにした場合、当たる確率は である。
これは、最初の選択時の確率がそのまま維持されるためである。
一方で、ドアを変更した場合の当たる確率は となる。
これは、最初の選択時において、プレイヤーが正解のドアを選ぶ確率は 、ハズレのドアを選ぶ確率は である。
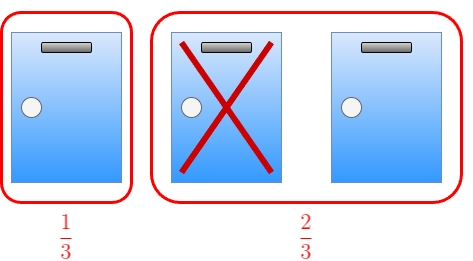
ここで重要なのは、モンティが知識を持ってハズレのドアを開けるという点である。
もし最初にハズレを選んでいた場合 ()、モンティは残りのドアから必ずもう1つのハズレを開けることになり、残った未開封のドアには必然的に正解が入っている。
つまり、この場合は変更すれば必ず正解に辿り着ける。
逆に、最初に正解を選んでいた場合 ()、モンティは残りのドアからどちらかのハズレを開け、変更すれば必ずハズレとなる。
この問題が示唆することは、単なる確率の計算を超えて、新しい情報 (モンティの行動) が与えられた場合に、どのように確率が変化するかという洞察を提供する。
また、人間の直感的な確率の理解と数学的な確率の計算の間にある大きなギャップを浮き彫りにする例としても知られている。
実際の実験やシミュレーションにおいても、変更戦略の方が勝率が高いことが確認されており、この問題は確率論において重要なものとして使用されている。
モンティホール問題の意味
3つのドアがあり、1つのドアの後ろに賞品 (車) があり、残りの2つのドアの後ろにはハズレ (ヤギ) がある。 プレイヤーが最初に1つのドアを選ぶ。 司会者 (モンティ) は、残りの2つのドアのうち、必ずハズレが入っているドアを1つ開けて見せる。 その後、プレイヤーは最初に選んだドアをそのままにする、あるいは、残りの閉じたドアに変更するかを選ぶ。
ここで重要な問題は、"ドアを変更した方が有利なのか"ということである。
結論からいうと、"ドアを変更した方が有利"である。
- そのままの場合
- 当たる確率は
- 変更した場合
- 当たる確率は
- 最初の選択時
- プレイヤーが正解のドアを選ぶ確率
- プレイヤーがハズレのドアを選ぶ確率
- モンティのドアを開けた後
- もし、最初にハズレを選んでいた場合 ( の確率)
- モンティは残りのドアのうち、必ずもう1つのハズレを開ける。
- つまり、残った未開封のドアには必ず正解が入っている。
- この場合、変更すれば必ず当たる。
- もし最初に正解を選んでいた場合 ( の確率)
- モンティは残りのドアのうち、どちらかのハズレを開ける。
- この場合、変更すると必ずハズレとなる。
したがって、
- 変更した場合の当たる確率 = 最初にハズレを選んでいた確率 =
- 変更しない場合の当たる確率 = 最初に正解を選んでいた確率 =
モンティホール問題のポイント
- モンティが知識を持っており、ハズレのドアを開けているという点
- 最初の選択時の確率 が、その後のモンティの行動によって変化するという点