「回路計算 - RL直列回路」の版間の差分
編集の要約なし |
|||
| 10行目: | 10行目: | ||
== 電流の求め方 == | == 電流の求め方 == | ||
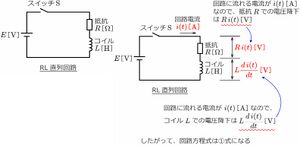
まず、RL直列回路の回路方程式をたてる。<br> | まず、RL直列回路の回路方程式をたてる。<br> | ||
[[ファイル:RL Circuit 1.jpg|フレームなし|中央]] | |||
<br> | <br> | ||
回路に流れる電流を<math>i(t)[A]</math>、<math>i(0) = 0[A]</math>とする時、次式(1)の微分方程式となる。<br> | 回路に流れる電流を<math>i(t)[A]</math>、<math>i(0) = 0[A]</math>とする時、次式(1)の微分方程式となる。<br> | ||
| 49行目: | 50行目: | ||
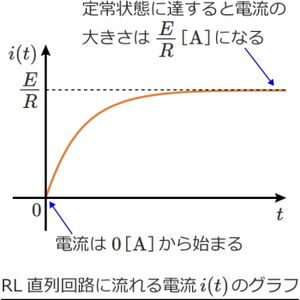
下図に示すように、RL直列回路に流れる電流i(t)は0から始まり、ある程度の時間が経過する(定常状態に達する)とE/Rの大きさの電流が流れ続ける。<br> | 下図に示すように、RL直列回路に流れる電流i(t)は0から始まり、ある程度の時間が経過する(定常状態に達する)とE/Rの大きさの電流が流れ続ける。<br> | ||
つまり、定常状態に達すると、コイルLは短絡されているのと同じということになる。<br> | つまり、定常状態に達すると、コイルLは短絡されているのと同じということになる。<br> | ||
[[ファイル:RL Circuit 2.jpg|フレームなし|中央]] | |||
<br> | <br> | ||
また、RL直列回路の時定数τは、<math>\tau = \frac{L}{R}</math>である。<br> | また、RL直列回路の時定数τは、<math>\tau = \frac{L}{R}</math>である。<br> | ||
| 70行目: | 72行目: | ||
<br> | <br> | ||
つまり、定常状態に達するとコイルLが無い場合と同様(コイルが短絡された状態と同じ)ということになる。<br> | つまり、定常状態に達するとコイルLが無い場合と同様(コイルが短絡された状態と同じ)ということになる。<br> | ||
[[ファイル:RL Circuit 3.jpg|フレームなし|中央]] | |||
<br><br> | <br><br> | ||
| 89行目: | 92行目: | ||
したがって、電源を投入した直後は、電源の電圧がすべてコイルLに掛かるが、定常状態に達すると、<br> | したがって、電源を投入した直後は、電源の電圧がすべてコイルLに掛かるが、定常状態に達すると、<br> | ||
コイルLには電圧がかからず、電源の電圧はすべて抵抗Rにかかる。<br> | コイルLには電圧がかからず、電源の電圧はすべて抵抗Rにかかる。<br> | ||
[[ファイル:RL Circuit 4.jpg|フレームなし|中央]] | |||
<br><br> | <br><br> | ||
__FORCETOC__ | __FORCETOC__ | ||
[[カテゴリ:回路計算]] | [[カテゴリ:回路計算]] | ||
2020年11月9日 (月) 09:17時点における最新版
概要
RL直列回路は電源を投入すると過渡現象が起こるため、回路に流れる電流は時間的に変化して、ある程度の時間が経過すると一定値になる。
このような時間的に変化する過渡現象の電圧や電流を求める時は、以下のような手順で解く。
- 対象の回路の回路方程式をたてる。
- 初期条件を考慮して微分方程式または積分方程式を解く。
ここでは、RL直列回路に流れる電流と電圧を、ラプラス変換を用いて求める。
電流の求め方
まず、RL直列回路の回路方程式をたてる。
回路に流れる電流を、とする時、次式(1)の微分方程式となる。
…(1)
(1)式をラプラス変換すると以下となる。
上式(2)において、部分分数分解を行う。
より、
となる。
したがって、(2)式は次式(3)に変形される。
最後に、上式(3)を逆ラプラス変換する。
したがって、RL直列回路に流れる電流i(t)は、時間が経つにつれて増加が緩やかになる。
下図に示すように、RL直列回路に流れる電流i(t)は0から始まり、ある程度の時間が経過する(定常状態に達する)とE/Rの大きさの電流が流れ続ける。
つまり、定常状態に達すると、コイルLは短絡されているのと同じということになる。
また、RL直列回路の時定数τは、である。
抵抗Rに掛かる電圧の求め方
RL直列回路に流れる電流i(t)は、上記のセクションで求めた式を使用する。
抵抗Rにかかる電圧ER(t)[V]は、次式となる。
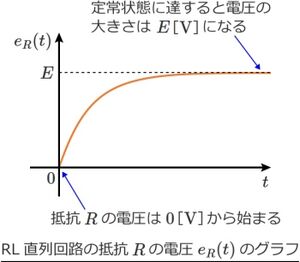
抵抗Rの電圧のグラフにおいて、電圧ER(t)はi(t)にRを乗算しただけなので、i(t)と同じような形のグラフになる。
抵抗Rの電圧は0[V]から始まり、ある程度時間が経過する(定常状態に達する)と、電圧の大きさはE[V]になる。
したがって、電源の電圧がすべて抵抗Rに掛かることになる。
つまり、定常状態に達するとコイルLが無い場合と同様(コイルが短絡された状態と同じ)ということになる。
コイルLに掛かる電圧の求め方
RL直列回路に流れる電流i(t)は、上記のセクションで求めた式を使用する。
コイルLにかかる電圧EL(t)[V]は、次式となる。
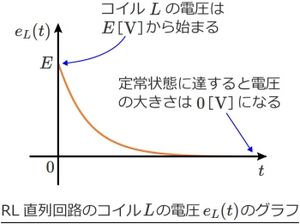
コイルLの電圧EL(t)のグラフは、電圧はE[V]から始まり、ある程度時間が経過する(定常状態に達する)と、電圧の大きさは0[V]になる。
したがって、電源を投入した直後は、電源の電圧がすべてコイルLに掛かるが、定常状態に達すると、
コイルLには電圧がかからず、電源の電圧はすべて抵抗Rにかかる。
![{\displaystyle i(t)[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81d8cda318f0d1460d4a4a4cf4cb4ce6a179bdf2)
![{\displaystyle i(0)=0[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03b7781d20f3598fe40bfd8223a08aed4f2cca24)