「第1回 グラフ理論の概要と応用」の版間の差分
| (同じ利用者による、間の1版が非表示) | |||
| 46行目: | 46行目: | ||
<br> | <br> | ||
点の次数(degree)とは、その点を端点とする辺の本数のことである。下図において、点Qの次数は4である。<br> | 点の次数(degree)とは、その点を端点とする辺の本数のことである。下図において、点Qの次数は4である。<br> | ||
[[ファイル:Graph Theory 1 1.jpg|フレームなし|中央]] | |||
<br> | <br> | ||
グラフとは点の集合とそれらの結び方の表現である。<br> | グラフとは点の集合とそれらの結び方の表現である。<br> | ||
| 53行目: | 54行目: | ||
以下の性質を満たすとき、2つのグラフは同形(あるいは同型)であると言う。<br> | 以下の性質を満たすとき、2つのグラフは同形(あるいは同型)であると言う。<br> | ||
片方のグラフで2つの点が結ばれる。 ⇔ 他方のグラフの対応している2点が結ばれる。<br> | 片方のグラフで2つの点が結ばれる。 ⇔ 他方のグラフの対応している2点が結ばれる。<br> | ||
[[ファイル:Graph Theory 1 2.jpg|フレームなし|中央]] | |||
<br> | <br> | ||
===== 多重辺 ループ 単純グラフ ===== | ===== 多重辺 ループ 単純グラフ ===== | ||
| 67行目: | 69行目: | ||
<br> | <br> | ||
閉路(cycle)とは、Q→S→T→Qのような形をした道のことである。(元の点に戻ってくる道)<br> | 閉路(cycle)とは、Q→S→T→Qのような形をした道のことである。(元の点に戻ってくる道)<br> | ||
[[ファイル:Graph Theory 1 3.jpg|フレームなし|中央]] | |||
<br> | <br> | ||
===== 特別な性質を持った歩道を含むグラフ ===== | ===== 特別な性質を持った歩道を含むグラフ ===== | ||
2020年3月9日 (月) 18:23時点における版
概要
- グラフ理論の周辺分野の概要について理解する。
- グラフの種類の概要について理解する。
- グラフ理論上の問題の概要について理解する。
- グラフ理論の応用分野の概要について理解する。
- グラフを用いた例題とその解法について理解する。
グラフ理論(Graph theory)とは
点や線を使った図形で問題を分析する数学(秋山 仁)
離散数学(情報科学)の1分野
起源
1736年のオイラーによるケーニヒスベルグの橋問題の解決(位相幾何学と共通の起源)
グラフ
点が辺で結ばれている構造のことである。
目的
グラフの持つ性質を明らかにする(数学的興味)とグラフを用いて抽象化される事象・現象の解析(工学的興味)
話題
- グラフの巡回性(ケーニヒスベルグの橋問題)
- グラフの平面性(彩色問題)
- マッチング理論(結婚問題)
- ネットワーク理論(輸送問題)
周辺分野
- 離散幾何学
- 計算幾何学
- 組み合わせ幾何学
- 離散数学
- 理論計算機科学
グラフ理論の概要
グラフとは
グラフとは、いくつかの点(vertex)が辺(edge)で結ばれている構造のことである。
グラフを用いて現象を抽象化すると、それらの現象をコンピュータ上で解析するのに役立つ。
グラフによる抽象化の例
コンピュータネットワーク、電子回路、分子構造、鉄道路線図など様々なものがグラフを用いて抽象化できる。
グラフの具体例
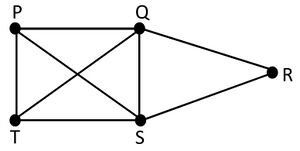
下図は、点P、Q、R、S、Tからなるグラフである。(辺PS、QTの交点はグラフの点ではない)
点の次数(degree)とは、その点を端点とする辺の本数のことである。下図において、点Qの次数は4である。
グラフとは点の集合とそれらの結び方の表現である。
したがって、距離的・空間的な性質とは無関係である。
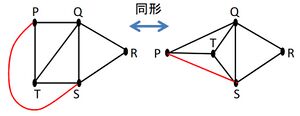
グラフ理論の観点からは、以下の2つのグラフは同じものとみなされる。
以下の性質を満たすとき、2つのグラフは同形(あるいは同型)であると言う。
片方のグラフで2つの点が結ばれる。 ⇔ 他方のグラフの対応している2点が結ばれる。
多重辺 ループ 単純グラフ
多重辺(multiple edge)とは、点Q、Sを結ぶ2本の辺のことである。
ループ(loop)とは、例えば、点Pを出て点Pに戻る辺のことである。
単純グラフ(simple graph)とは、多重辺やループを含まないグラフのことである。
歩道 道 閉路
歩道(walk)とは、ある点から別の点への行き方のことである。(連結した辺の列)
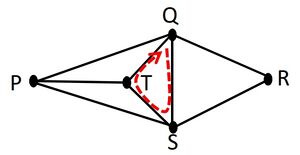
例 : 下図のグラフにおいて、P→Q→Rは長さ2の歩道で、P→S→Q→T→S→Rは長さ5の歩道である。
道(path)とは、どの点も高々一度しか現れない歩道のことである。
例 : 下図のグラフにおいて、P→T→S→Rは道である。
閉路(cycle)とは、Q→S→T→Qのような形をした道のことである。(元の点に戻ってくる道)
特別な性質を持った歩道を含むグラフ
オイラーグラフ(Eulerian graph)とは、全ての辺を1回ずつ通って元の点に戻る歩道を含むグラフのことである。
ハミルトングラフ(Hamilton graph)とは、全ての点を1回ずつ通って元の点に戻る歩道を含むグラフのことである。
連結グラフと非連結グラフ
連結グラフ(connected graph)とは、グラフがひとかたまりであり、どの2点も道で結ばれているようなグラフのことである。
非連結グラフ(disconnected graph)とは、2つ以上のかたまりからなるグラフのことである。
木
木(tree)とは、どの2点の間にも道が1本しかないような連結グラフのことである。(閉路のない連結グラフ)
平面的グラフ
平面的グラフ(planar graph)とは、交差がない同等なグラフに書き直せるグラフのことである。
平面的グラフは彩色問題で重要な役割を果たす。
彩色問題の重要な帰結として、4色定理がある。
平面的グラフの判定条件
以下の2種類の判定条件がある。
- 平面的グラフの部分グラフの性質に関する条件
- 双対性の概念に関連する条件
彩色問題と4色定理
彩色問題とは、単純グラフの点を、与えられた色数を用いて彩色し、どの辺の端点も異なる色になるようにできるかという問題である。
4色定理
平面的グラフは4彩色可能である。平面的グラフの場合、4色で点を彩色することが可能である。
点の彩色と(地図の)面の彩色の密接な関係が知られている。
4色定理の直観的意味
地図上の国を、同じ色の国は隣り合わないように4色で色分けすることが可能である。
2部グラフ
2部グラフ(bipartite graph)とは、点集合を2つの部分集合に分割して、各部分集合内の点同士の間には辺が無いグラフのことである。
これら点の集合を独立集合(independent set)という。(独立集合は2つある)
2部グラフは、結婚問題やHallの定理を議論する際に必要となる。
結婚問題
何人かの女性がそれぞれ何人かの男性と知り合っているとき、
どの女性も知り合いの男性と結婚できるように組み合わせるには、どんな条件が必要か。
Hallの定理
結婚問題に解があるための必要十分条件は、どのk人の女性も合わせてk人以上の男性と知り合いであることである。
ただし、であり、mは女性の数とする。
結婚問題とHallの定理は、グラフ理論の言葉でいうと、2部グラフの完全マッチングに関する問題および定理である。
Hallの定理は、男性集合と女性集合からなる2部グラフに対して、完全マッチングが存在するための必要十分条件を与えている。
結婚問題とHallの定理は、横断理論の言葉で表現することもできる。
有向グラフ
有向グラフ(directed graph, digraph)とは、辺に向きが付いているグラフのことである。
有向グラフは、ネットワークフローや輸送問題を議論する際に必要となる。
ネットワークフロー
辺に重みがついた重み付き有向グラフ(輸送ネットワーク)において、各点は工場や市場を表し、各辺は商品が送られるルートを表している。
各ルートにはルートを通過できる最大容量(重み)が与えられている。
輸送問題
上記のようなネットワークフローで表される状態を考えるとき、工場から市場まで最大でどれだけ商品を送れるか?
輸送問題に関連する有名な定理として、最大フロー・最小カット定理がある。
最大フロー・最小カット定理は、Hallの定理やMengerの定理と密接な関係がある。
グラフ理論の応用
最短路問題 最長路問題
最短路問題
与えられた路線図において、ある地点から別の地点まで最短距離で行く行き方を求める問題のことである。
最長路問題
与えられた路線図において、ある地点から別の地点まで最長距離で行く行き方を求める問題のことである。
例 : 紀行文 "最長片道切符の旅"
JRの片道切符で行ける最長のルート。北海道の広尾駅から出発し、鹿児島の枕崎駅まで13319kmの旅。
巡回セールスマン問題
全ての都市を1回ずつ通って元に戻ってくるルートはあるかという問題のことである。
その際、可能な限り合計距離を短くしたい。(距離や時間、費用を考慮したこの問題の変種が数多く研究されている)
例
中国の郵便配達員問題(巡回セールスマン問題やこの変種は、ハミルトン閉路を求めることに関係している)
産業関連グラフ問題
各産業は、他の産業からものを購入して生産活動を行っている。これら各産業の生産活動は、各産業を点とする有向グラフで表すことができる。
このようなグラフを産業関連グラフと言う。
ネットワークフローに関連する輸送問題も、産業関連グラフを使用した応用例である。
産業関連グラフに類似したグラフの例
- 持ち株グラフ
- 人口移動グラフ
- マッチング問題
- 完全マッチング問題(結婚問題やHallの定理に関連する問題で、2部グラフを使用する)
- 完全マッチングとは、例えば、婚活パーティーで全員がカップルになるようなペアの集まりのことである。
- 安定マッチング問題(安定結婚問題ともいい、2部グラフを使用する)
- 安定的マッチングとは、離婚する可能性の低いペアの集まりのことである。
- 現実的な応用が多数存在する問題で、医師臨床研修マッチング制度などがある。
インターネット関連グラフ問題
コンピュータを点とし、コンピュータ間の回線を辺で表すとインターネットのグラフができる。
このグラフの構造を調べることでインターネット上の様々な事象を解明しようとする研究がある。
例
- WWWにおけるハイパーリンクで繋がれたドキュメント全体の構造
- インターネットの接続構造
- SNSのコミュニティ構造
複雑ネットワーク問題
複雑ネットワークとは、現実世界に存在する巨大で複雑なネットワーク、
あるいはそれらネットワークの性質について考察する問題および分野のことである。
複雑ネットワークは、現実世界の様々な現象を説明するためのパラダイムの1つである。
例
- WWW
- 食物連鎖ネットワーク
- 論文の被引用関係ネットワーク
- 映画俳優の共演グラフ
- 線虫の神経回路網グラフ
- 送電網グラフ
複雑ネットワークの性質
- スモールワールド性(一見赤の他人に見えても、実際は中間に少数の人を介するだけで繋がっているという性質)
- スケールフリー性(一部の人は非常に多くの知人を持っているが、大多数の人々は知人の数は少ないという性質)
- クラスター性(多くの人が互いに知り合いであるようなグループが存在するという性質)
複雑ネットワークのグラフモデル
- スモールワールドモデル(スモールワールド性を持つグラフのモデル)
- バラバシ=アルバートモデル(スケールフリー性を持つグラフのモデル)
スモールワード現象
スモールワールド現象とは、世界中の人の中から任意に2人を選んだとき、その2人は驚くほど少ない知人を介して繋がっているという現象。
例
ベーコン数とは、アメリカの俳優ケヴィン・ベーコンと映画で共演したことのある俳優のベーコン数を1、
ベーコン数nの俳優と共演関係にある俳優のベーコン数をn + 1とする。
世界中の俳優のベーコン数を調べると大多数がベーコン数3から4の範囲に収まる。
スモールワールドネットワーク
スモールワールド現象に関連する具体的なグラフはスモールワールドネットワークと呼ばれる。
特徴
- 頂点の数に対して辺の数が少ない。
- 2頂点間の距離の平均は意外と小さい。
- 小さなクラスターがたくさんある。
病気の感染や噂の伝達が驚くほど速いのは、人々がスモールワールドネットワークで繋がっているからだと考えられている。
様々な事象をグラフで表すことのメリット
- グラフに表すことで、複雑な事象の全体が視覚的にとらえられ、理解しやすくなる。
- 全体の構造を把握しやすくなる。
- 各点の特徴がとらえやすくなる。
以上のメリットにより、社会の複雑な現象の解明に役立つ。