「第4回 - 2変数の回帰分析」の版間の差分
| 60行目: | 60行目: | ||
[[ファイル:Statistics 4 1.png|フレームなし|中央]] | [[ファイル:Statistics 4 1.png|フレームなし|中央]] | ||
<br> | <br> | ||
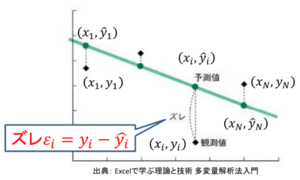
真値との誤差の2乗 <math>\epsilon_{i}^{2} = (y_i - \ | 真値との誤差の2乗 <math>\epsilon_{i}^{2} = (y_i - \hat{y_i})^{2}</math> の総和が最小になれば、直線モデル(回帰直線)が最良になる。<br> | ||
<br> | <br> | ||
元の値y<sub>i</sub>と回帰直線で推定した値 <math>\hat{y_i} = a x_i + b</math> の差(誤差 <math>\epsilon_{i}^{2} = (y_i - \hat{y_i})^2</math> )が最小になるようにするには、<br> | |||
全データの誤差の2乗(<math>\epsilon_{i}^{2} = (y_i - \hat{y_i})^{2}</math>)の和が最小になるように、直線の傾きaと切片bを決める。<br> | 全データの誤差の2乗(誤差<math>\epsilon_{i}^{2} = (y_i - \hat{y_i})^{2}</math>)の和が最小になるように、直線の傾きaと切片bを決める。<br> | ||
<br> | <br> | ||
これを、<u>最小2乗法</u>と呼ぶ。<br> | これを、<u>最小2乗法</u>と呼ぶ。<br> | ||
| 74行目: | 74行目: | ||
</math><br> | </math><br> | ||
<br> | <br> | ||
全データ組の誤差の2乗和S<sub>e</sub>を最小にする回帰係数a、bを求める。<br> | |||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| 82行目: | 82行目: | ||
</math><br> | </math><br> | ||
<br> | <br> | ||
上記の回帰係数を求めるには、S<sub>e</sub>の偏微分の結果が0となる鞍点を求める。<br> | |||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
2022年7月26日 (火) 02:31時点における版
概要
記述統計において、2変数間の相関がある時、
一方の変数xから他方の変数yの関係式を求める方法である回帰分析を学習する。
回帰分析とは
N個のデータの組x1、y1、...、xN、yNについて、
直線モデル(回帰直線) を当てはめて、データの分布を表す直線を計算することである。
これは、直線の傾きaと切片bを変化させて決める。
2変数間の相関係数rxyの絶対値が大きい場合に有効である。
以上のことから、回帰直線は次式となる。
回帰分析の使い道
- 回帰直線を使用して、yの推定に利用する。
- 代入するxの値には注意が必要である。
- 内挿 (問題なし)
- 外挿 (問題あり : 範囲外での推定精度は保証できないため)
- または
- ただし、外挿しても問題ない場合もあるため、推定結果が妥当かどうかを常に考えることが重要である。
- 内挿 (問題なし)
回帰分析の推定精度
回帰分析の推定精度を表すには、寄与率R2を用いる。
- 寄与率R2は、0〜1の範囲にあり、回帰直線の精度が高いほど寄与率は1に近づく。
- 相関係数rxyの2乗が寄与率R2に等しい。
回帰分析の原理
N個のデータの組(x1, y1)、...、(xN, yN)について、直線モデル(回帰直線)を当てはめる時、
実際には誤差があるため、元の値yiと回帰直線の式で推定した値 の差が最小になるようにしなくてはならない。
真値との誤差の2乗 の総和が最小になれば、直線モデル(回帰直線)が最良になる。
元の値yiと回帰直線で推定した値 の差(誤差 )が最小になるようにするには、
全データの誤差の2乗(誤差)の和が最小になるように、直線の傾きaと切片bを決める。
これを、最小2乗法と呼ぶ。
全データ組の誤差の2乗和Seを最小にする回帰係数a、bを求める。
上記の回帰係数を求めるには、Seの偏微分の結果が0となる鞍点を求める。
上記の2式を整理して次式とする。
これらを、正規方程式と呼ぶ。
… (1)
… (2)
上式を全データ組Nで除算する。
したがって、回帰直線の切片bは、傾きa、xの平均、yの平均で求めることができる。
を下式に代入する。
全データ組の誤差の2乗和Seが最小になる回帰係数は、
したがって、回帰直線は全データ組の平均値xとyを通る。
最小となったSeの値は、次式となる。