回路計算 - 電場と電位

概要

電場とは、電荷が周囲の空間に及ぼす影響を表す物理量である。
例えば、ある点に正の電荷を置いたときに、その電荷に働く電気力の大きさと向きを、電荷の大きさで割った値として定義される。
単位は、N/C (ニュートン毎クーロン) である。

電場は、電気力線として視覚的に表現される。
電気力線は正電荷から出て負電荷に入る曲線として描かれ、その密度が電場の強さを表す。
電気力線は決して交差せず、常に電場の向きを示す。

電位とは、電場内のある点に単位電荷を持ってくるのに必要な仕事量 (エネルギー) として定義される。
単位は、V (ボルト) である。

電位は基準点 (一般的には、無限遠点) からの相対的な値として表される。

電場と電位の関係性において、電位の空間的な変化率が電場の大きさを決定する。
数学的には、電場はスカラー量である電位の勾配 (空間微分) の負として表される。
つまり、電場は常に高電位から低電位に向かって形成される。

応用例として、コンデンサがある。
平行平板コンデンサ内部では、2つの平板間に一様な電場が形成され、電位は直線的に変化する。
この性質は、電子機器の設計や電気回路の様々な場面で活用されている。

また、電場と電位の概念では、例えば、雷は大気中での電位差が極めて大きくなることにより発生する放電現象として説明できる。

電場および電位において、ガウスの法則、等電位面等も関連しており、ガウスの法則は電荷分布から電場を求める時のツールとなる。

電場

電場とは、静電場において単位電荷を想定したときに受ける力のことであり、単位は[N/C]である。

${\vec {E}}={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {q}{r^{2}}}$ である。

ここで、ε₀とは真空中の誘電率のことであり、$8.854\dots \times 10^{-12}$ である。

電位

電位とは、静電場において単位電荷を想定したときに生じる位置エネルギーのことであり、単位は[V] = [J/C]である。

電位の特徴

• スカラー量

  電位はベクトルではなく、各点で単一の値を持つスカラー量である。

  これは、位置エネルギーがスカラー量であることに対応している。

• 相対的な量

  電位は必ず基準点 (多くの場合、無限遠点を0[V]とする) からの相対的な値として定義される。

  これは、位置エネルギーと同様の性質である。

電位は、ある点に単位の正電荷を無限遠から持ってくるのに必要な仕事量として解釈できる。
例えば、ある点の電位が5[V]であるということは、単位電荷 (1クーロン) をその点まで運ぶのに5[ジュール]の仕事が必要であることを意味する。

また、電位差 (電圧) は、2点間で電荷を移動させる際に必要なエネルギーを表す。

電場Eは単位電荷あたりの力、電位φは単位電荷あたりの位置エネルギーを表す。

一様な電界Eによる電位差Vの定義式:

$V={\vec {E}}d\quad {\mbox{[V]}}$

V [V] : 電位差
E [V/m] : 電界の強さ
d [m] : 長さ

電圧Vと仕事Wの関係

$W=qV\quad {\mbox{[J]}}$

W [J] : 仕事量
q [C] : 電荷
V [V] : 電位差

電位と電場の関係について

• 電場は、電位の空間的な変化率 (勾配の負) として定義される。

  ${\vec {E}}=-\nabla \phi$

  この関係は、電場が常に高電位から低電位へ向かうことを表現している。

• 電場の向きは、常に高電位から低電位に向かう。
• 等電位面上では、電場は常に等電位面に垂直となる。

平行平板コンデンサでは、2つの平板間に電位差をつけることで一様な電場が形成される。

クーロン力

電場E⃗の中で電荷qに働く力は、${\vec {F}}=q{\vec {E}}$ として表される。

ここで、${\vec {E}}={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {q}{r^{2}}}$ であるため、電荷q1およびq2とする時、
クーロン力は、 ${\vec {F}}=q_{1}{\vec {E}}={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {q_{1}q_{2}}{r^{2}}}$ となる。

重力場と静電場の対応関係

荷量 (スカラー) として、力学では質量m、電磁気学では電荷qを扱う。
場 (ベクトル) として、力学では重力加速度 ${\vec {g}}$、電磁気学では静電場 ${\vec {E}}$ を扱う。

したがって、これらの力積 (ベクトル) として、それぞれ重力 $m{\vec {g}}$ と静電気力 $q{\vec {E}}$ が得られる。

力学における重力と電磁気学における静電気力の間の類似性

	重力	(静) 電気力
荷量	質量 m [kg]	電荷 q [C]
場	重力加速度 ${\vec {g}}$ [m/s2]	静電場 ${\vec {E}}$ [N/C]
力	重力 $m{\vec {g}}$ [N]	静電気力 $q{\vec {E}}$ [N]

例題

例題 1 : 電位

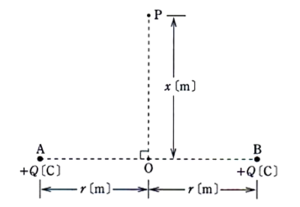
真空中において、下図に示すように点Oを通る直線上の点Oからそれぞれr[m]離れた2点A，BにQ[C]の正の点電荷が置かれている。
この直線に垂直で、点Oからx[m]離れた点Pの電位V[V]を表す式として、正しいのは次のうちどれか。

ただし、真空の誘電率をε0[F/m] とする。

距離AP、距離BPは、${\sqrt {r^{2}+x^{2}}}$ である。
距離AP、距離BPにおける電位Vは、$V_{AP}=V_{BP}={\vec {E}}d={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {Q}{\left({\sqrt {r^{2}+x^{2}}}\right)^{2}}}\times {\sqrt {r^{2}+x^{2}}}$

点電荷Aおよび点電荷Bが2つあるため、
$V={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {Q}{\left({\sqrt {r^{2}+x^{2}}}\right)^{2}}}\times {\sqrt {r^{2}+x^{2}}}\times 2$ より、
$V={\dfrac {1}{2\pi \epsilon _{0}}}{\dfrac {Q}{\sqrt {r^{2}+x^{2}}}}$ となる。

例題 2 : 電位

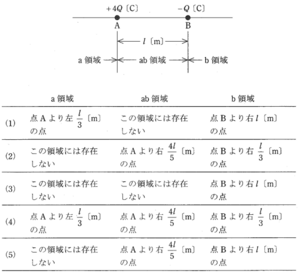
真空中において、下図のように点Aに正電荷+4Q[C]、点Bに負電荷-Q[C]の点電荷が配置されている。
この2点を通る直線上で電位が0[V]となる点を点Pとする。

点Pの位置を示すものとして、正しいものを組み合わせたのは次のうちどれか。
なお、無限遠の点は除く。

ただし、点Aと点B間の距離をl[m]とする。
また、点Aより左側の領域をa領域、点Aと点Bの間の領域をab領域、点Bより右側の領域をb領域とし、真空の誘電率をε0[F/m]とする。

• aの領域について
  

$V={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {4Q}{x}}+{\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {-Q}{x+l}}=0$ より、

${\begin{aligned}{\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {4Q}{x}}&={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {Q}{x+l}}\\{\dfrac {4Q}{x}}&={\dfrac {Q}{x+l}}\\{\dfrac {4}{x}}&={\dfrac {1}{x+l}}\\4(x+l)&=x\\4x+4l&=x\\3x&=-4l\\x&=-{\dfrac {4}{3}}l\end{aligned}}$

a領域では、$x$ は正である必要があるため、a領域には存在しない。

• ab領域について

$V={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {4Q}{x}}+{\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {-Q}{l-x}}=0$ より、
${\begin{aligned}{\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {4Q}{x}}&={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {Q}{l-x}}\\{\dfrac {4Q}{x}}&={\dfrac {Q}{l-x}}\\{\dfrac {4}{x}}&={\dfrac {1}{l-x}}\\4(l-x)&=x\\4l-4x&=x\\5x&=4l\\x&={\dfrac {4}{5}}l\end{aligned}}$

ab領域では、$x$ は正である必要があるため、${\dfrac {4}{5}}l$ となる。

• b領域について

$V={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {4Q}{l+x}}+{\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {-Q}{x}}=0$ より、
${\begin{aligned}{\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {4Q}{l+x}}&={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {Q}{x}}\\{\dfrac {4Q}{l+x}}&={\dfrac {Q}{x}}\\{\dfrac {4}{l+x}}&={\dfrac {1}{x}}\\4x&=l+x\\3x&=l\\x&={\dfrac {1}{3}}l\end{aligned}}$

b領域では、$x$ は正である必要があるため、${\dfrac {1}{3}}l$ となる。

例題 3 : 電位

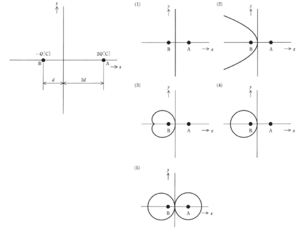
真空中において、下図のようにx軸上で、距離3d[m]隔てた点Ａ(2d，0)、点Ｂ(-d，0)にそれぞれ2Q[C]，-Q[C]の点電荷が置かれている。
xy平面上で、電位が0[V]となる等電位線を表す図として、最も近いものを次の(1)～(5)のうちから1つ選べ。

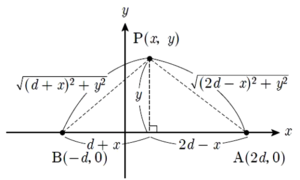
任意の点Pと点Aおよび点Bまでの距離は、下図のようになる。

点電荷Q[C]のr[m]離れた地点における電位V[V]は、${\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {Q}{r}}$ で表すことができる。

任意の点P(x，y)の電位をV_P[V]とする時、V_P[V]は点Aによる点Pの電位V_PA[V]と、点Bによる点Pの電位V_PB[V]のスカラ和となる。
${\begin{aligned}V_{P}&=V_{PA}+V_{PB}\\&={\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {Q}{r}}+{\dfrac {1}{4\pi \epsilon _{0}}}{\dfrac {-Q}{BP}}\\&={\dfrac {Q}{4\pi \epsilon _{0}}}\left({\dfrac {2}{\sqrt {(2d-x)^{2}+y^{2}}}}-{\dfrac {1}{\sqrt {(d+x)^{2}+y^{2}}}}\right)\end{aligned}}$

$V_{P}=0{\mbox{[V]}}$ となるには、
${\dfrac {2}{\sqrt {(2d-x)^{2}+y^{2}}}}-{\dfrac {1}{\sqrt {(d+x)^{2}+y^{2}}}}=0$ の時である。

したがって、
${\begin{aligned}{\dfrac {4}{(2d-x)^{2}+y^{2}}}-{\dfrac {1}{(d+x)^{2}+y^{2}}}&=0\\(2d-x)^{2}+y^{2}-4((d+x)^{2}+y^{2})&=0\\4d^{2}-4dx+x^{2}+y^{2}-4y^{2}-4(d+x)^{2}&=0\\4d^{2}-4dx+x^{2}+y^{2}-4y^{2}-4x^{2}-8dx-4d^{2}&=0\\-3x^{2}-3y^{2}-12dx&=0\\x^{2}+y^{2}+4dx&=0\\\end{aligned}}$

上式より、
${\begin{aligned}(x+2d)^{2}-4d^{2}+y^{2}+4dx&=0\\(x+2d)^{2}+y^{2}&=(2d)^{2}\end{aligned}}$
と変形できる。

この式は、中心 $(-2d,0)$ で半径が $2d$ の円の方程式である。