「データベース - 正規化」の版間の差分
(ページの作成:「== 概要 == データベースの正規化とは、データを扱いやすくするために行うデータベース設計の理論である。<br> <br> 1データ1箇所の原則を実現するため、1970年にE.F.Codd氏がリレーショナルモデルの理論として提案された。<br> 正規化の理論は、データの冗長性を排除し、更新時の整合性を維持しやすくすることを目指している。<br> <br> データベースは…」) |
|||
| (同じ利用者による、間の24版が非表示) | |||
| 24行目: | 24行目: | ||
==== 推移従属 ==== | ==== 推移従属 ==== | ||
推移従属とは、エンティティの3つの属性A、B、Cにおいて、<u>A -> B、 B ≠ A、 B -> Cである</u>時、 A -> Cが得られ、既存の関数従属から新たな関数従属が得られる状態を表す。<br> | 推移従属とは、エンティティの3つの属性A、B、Cにおいて、<u>A -> B、 B ≠ A、 B -> Cである</u>時、 A -> Cが得られ、既存の関数従属から新たな関数従属が得られる状態を表す。<br> | ||
<br> | |||
==== 多値従属性 ==== | |||
集合A、B、Cを集合Rの属性集合の任意の部分集合とする。<br> | |||
集合Rのある(A値, C値)対に対応するB値の集合がA値だけに依存しており、C値には独立の時、集合Bは集合Aに多値従属しているという。<br> | |||
<br><br> | <br><br> | ||
| 30行目: | 34行目: | ||
一般的には、第3正規化までを実施すればよいと云われているが、理論に当てはまる場合には第5正規化まで行う必要がある。<br> | 一般的には、第3正規化までを実施すればよいと云われているが、理論に当てはまる場合には第5正規化まで行う必要がある。<br> | ||
<br> | <br> | ||
[[ファイル:Database Normalization 1.png|フレームなし|中央]] | |||
<center>図. 正規化の手順</center><br> | <center>図. 正規化の手順</center><br> | ||
<br><br> | <br><br> | ||
== 非正規形 | == 非正規形 == | ||
==== 非正規形とは ==== | ==== 非正規形とは ==== | ||
現実の世界では、データは属性の集合として存在している。<br> | 現実の世界では、データは属性の集合として存在している。<br> | ||
| 42行目: | 46行目: | ||
一般的に、これらの属性は正規化されていないため、<u>非正規形</u>と呼ぶ。<br> | 一般的に、これらの属性は正規化されていないため、<u>非正規形</u>と呼ぶ。<br> | ||
<br> | <br> | ||
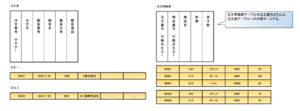
下図に示す受注伝票を例にして、正規化の手順を実施する。<br> | |||
[[ファイル:Database Normalization 2.png|フレームなし|中央]] | |||
<center>図. 受注伝票</center><br> | |||
<br> | |||
==== 導出属性 ==== | ==== 導出属性 ==== | ||
導出属性は、正規化の作業を行う場合、取り除くのが原則である。<br> | 導出属性は、正規化の作業を行う場合、取り除くのが原則である。<br> | ||
| 50行目: | 59行目: | ||
この非正規形のデータ集合を表の形に成形する。<br> | この非正規形のデータ集合を表の形に成形する。<br> | ||
<br> | <br> | ||
[[ファイル:Database Normalization 3.png|フレームなし|中央]] | |||
<center>図. 非正規形のデータ集合を表の形に成形</center><br> | <center>図. 非正規形のデータ集合を表の形に成形</center><br> | ||
<br> | <br> | ||
| 57行目: | 67行目: | ||
<br> | <br> | ||
下図に、非正規形のデータを表の形に成形している。<br> | 下図に、非正規形のデータを表の形に成形している。<br> | ||
[[ファイル:Database Normalization 4.png|フレームなし|中央]] | |||
<center>図. 表として成形</center><br> | |||
<br><br> | |||
== 第1正規化 == | |||
==== 第1正規化とは ==== | |||
第1正規化では、同一の情報のグループが繰り返し出現している部分を分解する。<br> | |||
その結果、第1正規形は、繰り返しの配列構造が排除された構造となる。<br> | |||
<br> | |||
==== 第1正規化の手順 ==== | |||
* 重複の削除 | |||
*: 同じ属性が繰り返されている部分の重複を削除する。 | |||
*: この時、細かい複数の表に分解されるため、元の表と結合できるように、分解した表に元の表のキー項目(主キー)を外部キーとする。 | |||
*: <br> | |||
*: まず、属性が繰り返し出現するグループを別の表に分解して、元の表に残った行と、分解した繰り返し出現するグループの行を一意に決められる主キーをそれぞれ定義する。 | |||
*: 次に、 分解した表の行と元の表の関係を維持することを目的として、分解先の表に元の表と結合できるようにキー項目(外部キー)を定義する。 | |||
<br> | |||
==== 例: 受注伝票の第1正規化 ==== | |||
# 元の表(注文表)の"注文番号"をキーとする。 | |||
# 下図に示すように、繰り返し出現するグループを分解して(注文明細表)、主キーをそれぞれ"注文番号"および"商品番号"とする。(複合キーとする) | |||
# 分解した注文明細表と注文表との関係は、注文明細表に取り込んだ"注文番号"を使用して参照できるようにする。 | |||
# 注文明細表の注文番号は、注文表への外部キーとする。 | |||
<br> | |||
[[ファイル:Database Normalization 5.png|フレームなし|中央]] | |||
<center>図. 第1正規形 </center><br> | |||
<br><br> | |||
== 第2正規化 == | |||
==== 第2正規化 ==== | |||
第2正規化で焦点となるのは、主キーと主キー以外の属性との関係である。<br> | |||
<br> | |||
例えば、注文明細表の"単価"と"受注数"は主キーにより一意に特定できるが、その決定方法は異なる。<br> | |||
"受注数"は、主キーを構成する"注文番号"および"商品番号"のどちらの属性が欠けても一意に特定できないが、"単価"は"商品番号"があれば一意に特定できる。<br> | |||
表の主キーの全てを必要とせず、"主キーの一部"のみで一意に指定可能な属性が存在する場合、その部分を別の表に分解することができる。<br> | |||
<br> | |||
これが、第2正規化である。<br> | |||
<br> | |||
==== 第2正規化の手順 ==== | |||
# 主キーが複数の列で構成されている複合主キーの表を対象とする。 | |||
# 複合主キーの一部に関数従属関係を持つ属性を洗い出し、別の表に分解する。 | |||
# 分解した表の行と元の表の行の関係を維持できるように、分解した表のキー項目(外部キー)を定義する。 | |||
<br> | |||
==== 例: 受注伝票と関数従属 ==== | |||
注文明細表の"単価"は、複合主キーである"注文番号"と"商品番号"に完全従属していない。<br> | |||
しかし、注文明細表の"単価"は、複合主キーの1つである"商品番号"にのみ部分従属している。<br> | |||
<br> | |||
==== 例: 受注伝票の第1正規化から第2正規化 ==== | |||
# 注文明細表が対象となる。 | |||
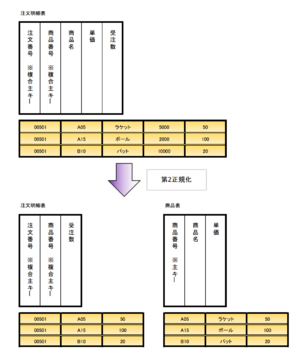
# 下図のように分解する。<br><br>注文明細表の主キーは、"注文番号"および"商品番号"の複合主キーである。<br>商品表の主キーは、"商品番号"である。 | |||
#: [[ファイル:Database Normalization 6.png|フレームなし|中央]] | |||
#: <center>図. 第2正規形</center><br> | |||
#: <br> | |||
# 注文明細表の"商品番号"は、商品表を参照する外部キーとして定義する。 | |||
<br><br> | |||
== 第3正規形 == | |||
==== 第3正規形とは ==== | |||
第2正規形から主キー以外の属性が相互に依存関係をもたないようにする作業が第3正規化である。<br> | |||
つまり、非キー項目同士の関数従属関係がある場合は、それを取り除く必要がある。<br> | |||
<br> | |||
第3正規形の条件は、第2正規形から推移的関数従属を含まないことである。<br> | |||
<br> | |||
* 推移関数従属とは | |||
*: 推移関数従属とは、非キー属性から非キー属性が導かれることである。 | |||
*: <br> | |||
*: 例えば、重複しない属性X、Y、Zがあり、属性Xは主キー、属性YおよびZは非キー属性であるとする。 | |||
*: ここで、<math>X \rightarrow Y \rightarrow Z</math> と推移的に導かれる場合、推移関数従属であるという。 ( <math>X \rightarrow Z</math> が成り立つ) | |||
*: <br> | |||
*: この例では、属性Yは属性Xに関数従属であり、属性Zは属性Yに関数従属であり、属性Xは属性Yに関数従属でないため、属性Zは属性Xに推移関数従属である。 | |||
<br> | |||
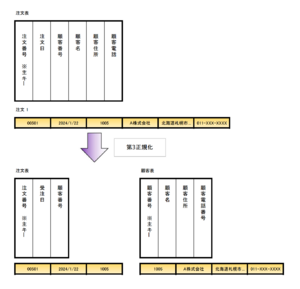
例えば、注文伝票において、"顧客住所"と"顧客電話番号"は"注文番号"から直接決定されるわけではなく、"顧客情報"という独立した要素の一部である。<br> | |||
注文表の非キー項目である"顧客番号"から決定される"顧客名"や"顧客住所"のような関係を<u>推移関数従属がある</u>という。<br> | |||
<br> | |||
==== 第3正規形の手順 ==== | |||
# 全ての表の主キー以外の属性間の関数従属関係が対象となる。 | |||
# 従属関係をもつ属性を洗い出し、別の表に分解する。 | |||
# 分解した表の行と元の表の行の関係を維持することができるように、表のキー項目(外部キー)を定義する。 | |||
<br> | |||
[[ファイル:Database Normalization 7.png|フレームなし|中央]] | |||
<center>図. 第3正規形</center><br> | |||
<br><br> | |||
== ボイスコッド正規形 (第3.5正規形) == | |||
==== ボイスコッド正規形とは ==== | |||
ボイスコッド正規形は、第3正規形をさらに分解したものである。<br> | |||
主キー以外のカラムが全て主キーに完全関数従属であり、それ以外の従属関係がある場合、表を分離することによりボイスコッド正規形となる。<br> | |||
<br> | |||
ボイスコッド正規形では、全ての属性が候補キーに完全従属する。<br> | |||
ボイスコッド正規形は、ほとんどの場合において第3正規形と等価であり、複数の属性からなる候補キーが複数存在する場合にのみ差異が生じうる。<br> | |||
<br> | |||
第3正規形とボイスコッド正規形の違いを、以下に示す。<br> | |||
* 第3正規形 | |||
*: 非キー属性を従属項とする関数従属性だけを問題とするため、候補キーを構成する属性の間に候補キーを決定項としない関数従属性が存在することを許す。 | |||
* ボイスコッド正規形 | |||
*: この問題が存在することを許さない。 | |||
<br> | |||
そのため、ボイスコッド正規形は、第3正規形をより完全にしたものであるといえる。<br> | |||
<br> | |||
<u>ただし、ボイスコッド正規形では、分解により一部失われるデータが発生する場合がある。</u><br> | |||
<br> | |||
< | ==== ボイスコッド正規形の手順 ==== | ||
例えば、受注伝票に顧客のメールアドレスが含まれているとする。<br> | |||
商品の購入時に登録済みのメールアドレスを再登録する場合はエラーとする場合、顧客名とメールアドレスは1:1の関係となる。<br> | |||
<br> | |||
この場合、ボイスコッド正規形ではテーブルを2つに分離することになる。<br> | |||
<br><br> | <br><br> | ||
== 第4正規形 == | |||
==== 第4正規形とは ==== | |||
第4正規化では、ボイスコッド正規形等を適用して3つ以上の主キーのみで構成されたテーブルから、さらに主キーを分解して、多値従属性を排除する処理を行う。<br> | |||
<br> | |||
多値従属性とは、属性Xが1つ決まれば他の属性が1つ以上決まる性質のことである。<br> | |||
<br> | |||
下表では、社員ID、部門コード、氏名を主キーとしており、社員IDが決定する時、部門コードと氏名の2つの属性がそれぞれ複数決定される。<br> | |||
複数の多値従属性が存在しているため、これらを排除すれば第4正規形となる。<br> | |||
<center> | |||
{| class="wikitable" style="background-color:#fefefe;" | |||
|- | |||
! style="background-color:#66CCFF; width: 200px;" | 社員ID | |||
! style="background-color:#66CCFF; width: 200px;" | 部門コード | |||
! style="background-color:#66CCFF; width: 200px;" | 氏名 | |||
|- | |||
| A001 || 1001 || 田中一郎 | |||
|- | |||
| A010 || 1010 || 山田太郎 | |||
|- | |||
| B005 || 2005 || 鈴木一夫 | |||
|- | |||
| C100 || 3100 || 佐藤次郎 | |||
|} | |||
</center> | |||
<br> | |||
<center> | |||
{| class="wikitable" style="background-color:#fefefe;" | |||
|- | |||
| | |||
{| class="wikitable" style="background-color:#fefefe; width: 350px; margin: 15px;" | |||
|- | |||
! style="background-color:#66CCFF; width: 50%;" | 社員ID | |||
! style="background-color:#66CCFF; width: 50%;" | 部門コード | |||
|- | |||
| A001 || 1001 | |||
|- | |||
| A010 || 1010 | |||
|- | |||
| B005 || 2005 | |||
|- | |||
| C100 || 3100 | |||
|} | |||
| | |||
{| class="wikitable" style="background-color:#fefefe; width: 350px; margin: 15px;" | |||
|- | |||
! style="background-color:#66CCFF; width: 50%;" | 社員ID | |||
! style="background-color:#66CCFF; width: 50%;" | 氏名 | |||
|- | |||
| A001 || 田中一郎 | |||
|- | |||
| A010 || 山田太郎 | |||
|- | |||
| B005 || 鈴木一夫 | |||
|- | |||
| C100 || 佐藤次郎 | |||
|} | |||
|} | |||
</center> | |||
<br> | |||
==== 第4正規形の手順 ==== | |||
https://ja.wikipedia.org/wiki/%E9%96%A2%E4%BF%82%E3%81%AE%E6%AD%A3%E8%A6%8F%E5%8C%96<br> | |||
<br><br> | |||
== 第5正規形 == | |||
==== 第5正規形とは ==== | |||
第5正規化とは、射影-結合正規形とも呼ばれており、<br> | |||
第4正規形と同様、3つ以上の主キーのみで構成されたテーブルからさらに主キーを分解して、候補キーの中で結合従属性が満足できるようにする。<br> | |||
したがって、結合従属性を含まないようにする必要がある。<br> | |||
<br> | |||
結合従属性とは、多値従属性が2つに分解できるのに対して、それ以上に分解できる場合のことである。<br> | |||
<br> | |||
下表では、{支店} -> {在庫商品}、{支店} -> {メーカー}、{在庫商品} -> {メーカー}と3つの関係を含んでいるため、3つに分解可能である。<br> | |||
<center> | |||
{| class="wikitable" style="background-color:#fefefe;" | |||
|- | |||
! style="background-color:#66CCFF; width: 200px;" | 支店 | |||
! style="background-color:#66CCFF; width: 200px;" | 在庫商品 | |||
! style="background-color:#66CCFF; width: 200px;" | メーカー | |||
|- | |||
| 東京 || テレビ || A社 | |||
|- | |||
| 東京 || テレビ || B社 | |||
|- | |||
| 東京 || エアコン || A社 | |||
|- | |||
| 愛知 || 冷蔵庫 || C社 | |||
|} | |||
</center> | |||
<br> | |||
<center> | |||
{| class="wikitable" style="background-color:#fefefe;" | |||
|- | |||
| | |||
{| class="wikitable" style="background-color:#fefefe; width: 350px; margin: 15px;" | |||
|- | |||
! style="background-color:#66CCFF; width: 50%;" | 支店 | |||
! style="background-color:#66CCFF; width: 50%;" | 在庫商品 | |||
|- | |||
| 東京 || テレビ | |||
|- | |||
| 東京 || テレビ | |||
|- | |||
| 東京 || エアコン | |||
|- | |||
| 愛知 || 冷蔵庫 | |||
|} | |||
| | |||
{| class="wikitable" style="background-color:#fefefe; width: 350px; margin: 15px;" | |||
|- | |||
! style="background-color:#66CCFF; width: 50%;" | 支店 | |||
! style="background-color:#66CCFF; width: 50%;" | 仕入先 | |||
|- | |||
| 東京 || A社 | |||
|- | |||
| 東京 || B社 | |||
|- | |||
| 東京 || A社 | |||
|- | |||
| 愛知 || C社 | |||
|} | |||
| | |||
{| class="wikitable" style="background-color:#fefefe; width: 350px; margin: 15px;" | |||
|- | |||
! style="background-color:#66CCFF; width: 50%;" | 商品 | |||
! style="background-color:#66CCFF; width: 50%;" | メーカー | |||
|- | |||
| テレビ || A社 | |||
|- | |||
| テレビ || B社 | |||
|- | |||
| エアコン || A社 | |||
|- | |||
| 冷蔵庫 || C社 | |||
|} | |||
|} | |||
</center> | |||
<br> | |||
==== 第5正規形の手順 ==== | |||
https://ja.wikipedia.org/wiki/%E9%96%A2%E4%BF%82%E3%81%AE%E6%AD%A3%E8%A6%8F%E5%8C%96<br> | |||
<br><br> | |||
{{#seo: | |||
|title={{PAGENAME}} : Exploring Electronics and SUSE Linux | MochiuWiki | |||
|keywords=MochiuWiki,Mochiu,Wiki,Mochiu Wiki,Electric Circuit,Electric,pcb,Mathematics,AVR,TI,STMicro,AVR,ATmega,MSP430,STM,Arduino,Xilinx,FPGA,Verilog,HDL,PinePhone,Pine Phone,Raspberry,Raspberry Pi,C,C++,C#,Qt,Qml,MFC,Shell,Bash,Zsh,Fish,SUSE,SLE,Suse Enterprise,Suse Linux,openSUSE,open SUSE,Leap,Linux,uCLnux,Podman,電気回路,電子回路,基板,プリント基板 | |||
|description={{PAGENAME}} - 電子回路とSUSE Linuxに関する情報 | This page is {{PAGENAME}} in our wiki about electronic circuits and SUSE Linux | |||
|image=/resources/assets/MochiuLogo_Single_Blue.png | |||
}} | |||
__FORCETOC__ | __FORCETOC__ | ||
[[カテゴリ:SQL_Server]][[カテゴリ:MySQL]] | [[カテゴリ:SQL_Server]][[カテゴリ:MySQL]] | ||
2024年11月10日 (日) 15:51時点における最新版
概要
データベースの正規化とは、データを扱いやすくするために行うデータベース設計の理論である。
1データ1箇所の原則を実現するため、1970年にE.F.Codd氏がリレーショナルモデルの理論として提案された。
正規化の理論は、データの冗長性を排除し、更新時の整合性を維持しやすくすることを目指している。
データベースは常にレコードが追加、更新、削除されている。
もし、正規化を適切に行っていない場合は、データベースのレコード間で矛盾が発生して、データベースとして役割を果たさない。
データベースの正規化の目的は、データの重複や不要な依存関係を排除することである。
これにより、データの整合性を維持できるようになる。
関数従属
関数従属とは
ある属性Aの値が決まると他の属性Bの値が一意に決まる時、属性Bは、属性Aに関数従属である (A -> B) という。
完全従属
完全従属とは、2つの属性A、Bの間でA -> Bが成立して、Aが複数の属性の集合で成り立っている場合、属性Aのいかなる部分集合も関数従属が成立しない状態を表す。
部分従属
部分従属とは、関数従属が成立しているが、完全従属ではない状態を表す。
推移従属
推移従属とは、エンティティの3つの属性A、B、Cにおいて、A -> B、 B ≠ A、 B -> Cである時、 A -> Cが得られ、既存の関数従属から新たな関数従属が得られる状態を表す。
多値従属性
集合A、B、Cを集合Rの属性集合の任意の部分集合とする。
集合Rのある(A値, C値)対に対応するB値の集合がA値だけに依存しており、C値には独立の時、集合Bは集合Aに多値従属しているという。
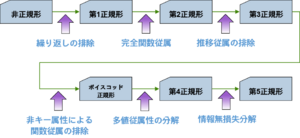
正規化の手順
正規化は、データの一元管理を行うために、データベース設計で行うべき理論である。
一般的には、第3正規化までを実施すればよいと云われているが、理論に当てはまる場合には第5正規化まで行う必要がある。
非正規形
非正規形とは
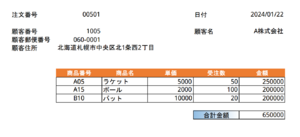
現実の世界では、データは属性の集合として存在している。
例えば、注文伝票や納品伝票等の形で存在しているデータは、属性の集合ということができる。
一般的に、これらの属性は正規化されていないため、非正規形と呼ぶ。
下図に示す受注伝票を例にして、正規化の手順を実施する。
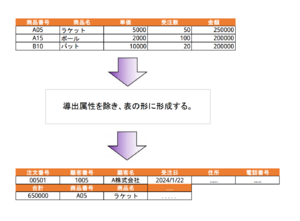
導出属性
導出属性は、正規化の作業を行う場合、取り除くのが原則である。
ただし、実際の設計では、管理項目を上流工程で削除する場合、元々管理されていた属性を失い、後で復旧することは困難となる。
そこで、導出属性である旨を明記した上でER図に記述する。
この非正規形のデータ集合を表の形に成形する。
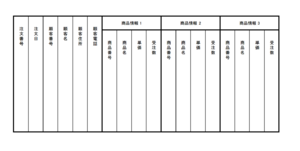
表の形に成形する場合、表の定義として以下に示す2点に注意する。
- 表を定義する列は、1列につき1つのみとする。
- 表の各行を特定できるキー列(一意識別子)を考える。
下図に、非正規形のデータを表の形に成形している。
第1正規化
第1正規化とは
第1正規化では、同一の情報のグループが繰り返し出現している部分を分解する。
その結果、第1正規形は、繰り返しの配列構造が排除された構造となる。
第1正規化の手順
- 重複の削除
- 同じ属性が繰り返されている部分の重複を削除する。
- この時、細かい複数の表に分解されるため、元の表と結合できるように、分解した表に元の表のキー項目(主キー)を外部キーとする。
- まず、属性が繰り返し出現するグループを別の表に分解して、元の表に残った行と、分解した繰り返し出現するグループの行を一意に決められる主キーをそれぞれ定義する。
- 次に、 分解した表の行と元の表の関係を維持することを目的として、分解先の表に元の表と結合できるようにキー項目(外部キー)を定義する。
例: 受注伝票の第1正規化
- 元の表(注文表)の"注文番号"をキーとする。
- 下図に示すように、繰り返し出現するグループを分解して(注文明細表)、主キーをそれぞれ"注文番号"および"商品番号"とする。(複合キーとする)
- 分解した注文明細表と注文表との関係は、注文明細表に取り込んだ"注文番号"を使用して参照できるようにする。
- 注文明細表の注文番号は、注文表への外部キーとする。
第2正規化
第2正規化
第2正規化で焦点となるのは、主キーと主キー以外の属性との関係である。
例えば、注文明細表の"単価"と"受注数"は主キーにより一意に特定できるが、その決定方法は異なる。
"受注数"は、主キーを構成する"注文番号"および"商品番号"のどちらの属性が欠けても一意に特定できないが、"単価"は"商品番号"があれば一意に特定できる。
表の主キーの全てを必要とせず、"主キーの一部"のみで一意に指定可能な属性が存在する場合、その部分を別の表に分解することができる。
これが、第2正規化である。
第2正規化の手順
- 主キーが複数の列で構成されている複合主キーの表を対象とする。
- 複合主キーの一部に関数従属関係を持つ属性を洗い出し、別の表に分解する。
- 分解した表の行と元の表の行の関係を維持できるように、分解した表のキー項目(外部キー)を定義する。
例: 受注伝票と関数従属
注文明細表の"単価"は、複合主キーである"注文番号"と"商品番号"に完全従属していない。
しかし、注文明細表の"単価"は、複合主キーの1つである"商品番号"にのみ部分従属している。
例: 受注伝票の第1正規化から第2正規化
- 注文明細表が対象となる。
- 下図のように分解する。
注文明細表の主キーは、"注文番号"および"商品番号"の複合主キーである。
商品表の主キーは、"商品番号"である。図. 第2正規形
- 注文明細表の"商品番号"は、商品表を参照する外部キーとして定義する。
第3正規形
第3正規形とは
第2正規形から主キー以外の属性が相互に依存関係をもたないようにする作業が第3正規化である。
つまり、非キー項目同士の関数従属関係がある場合は、それを取り除く必要がある。
第3正規形の条件は、第2正規形から推移的関数従属を含まないことである。
- 推移関数従属とは
- 推移関数従属とは、非キー属性から非キー属性が導かれることである。
- 例えば、重複しない属性X、Y、Zがあり、属性Xは主キー、属性YおよびZは非キー属性であるとする。
- ここで、 と推移的に導かれる場合、推移関数従属であるという。 ( が成り立つ)
- この例では、属性Yは属性Xに関数従属であり、属性Zは属性Yに関数従属であり、属性Xは属性Yに関数従属でないため、属性Zは属性Xに推移関数従属である。
例えば、注文伝票において、"顧客住所"と"顧客電話番号"は"注文番号"から直接決定されるわけではなく、"顧客情報"という独立した要素の一部である。
注文表の非キー項目である"顧客番号"から決定される"顧客名"や"顧客住所"のような関係を推移関数従属があるという。
第3正規形の手順
- 全ての表の主キー以外の属性間の関数従属関係が対象となる。
- 従属関係をもつ属性を洗い出し、別の表に分解する。
- 分解した表の行と元の表の行の関係を維持することができるように、表のキー項目(外部キー)を定義する。
ボイスコッド正規形 (第3.5正規形)
ボイスコッド正規形とは
ボイスコッド正規形は、第3正規形をさらに分解したものである。
主キー以外のカラムが全て主キーに完全関数従属であり、それ以外の従属関係がある場合、表を分離することによりボイスコッド正規形となる。
ボイスコッド正規形では、全ての属性が候補キーに完全従属する。
ボイスコッド正規形は、ほとんどの場合において第3正規形と等価であり、複数の属性からなる候補キーが複数存在する場合にのみ差異が生じうる。
第3正規形とボイスコッド正規形の違いを、以下に示す。
- 第3正規形
- 非キー属性を従属項とする関数従属性だけを問題とするため、候補キーを構成する属性の間に候補キーを決定項としない関数従属性が存在することを許す。
- ボイスコッド正規形
- この問題が存在することを許さない。
そのため、ボイスコッド正規形は、第3正規形をより完全にしたものであるといえる。
ただし、ボイスコッド正規形では、分解により一部失われるデータが発生する場合がある。
ボイスコッド正規形の手順
例えば、受注伝票に顧客のメールアドレスが含まれているとする。
商品の購入時に登録済みのメールアドレスを再登録する場合はエラーとする場合、顧客名とメールアドレスは1:1の関係となる。
この場合、ボイスコッド正規形ではテーブルを2つに分離することになる。
第4正規形
第4正規形とは
第4正規化では、ボイスコッド正規形等を適用して3つ以上の主キーのみで構成されたテーブルから、さらに主キーを分解して、多値従属性を排除する処理を行う。
多値従属性とは、属性Xが1つ決まれば他の属性が1つ以上決まる性質のことである。
下表では、社員ID、部門コード、氏名を主キーとしており、社員IDが決定する時、部門コードと氏名の2つの属性がそれぞれ複数決定される。
複数の多値従属性が存在しているため、これらを排除すれば第4正規形となる。
| 社員ID | 部門コード | 氏名 |
|---|---|---|
| A001 | 1001 | 田中一郎 |
| A010 | 1010 | 山田太郎 |
| B005 | 2005 | 鈴木一夫 |
| C100 | 3100 | 佐藤次郎 |
|
|
第4正規形の手順
https://ja.wikipedia.org/wiki/%E9%96%A2%E4%BF%82%E3%81%AE%E6%AD%A3%E8%A6%8F%E5%8C%96
第5正規形
第5正規形とは
第5正規化とは、射影-結合正規形とも呼ばれており、
第4正規形と同様、3つ以上の主キーのみで構成されたテーブルからさらに主キーを分解して、候補キーの中で結合従属性が満足できるようにする。
したがって、結合従属性を含まないようにする必要がある。
結合従属性とは、多値従属性が2つに分解できるのに対して、それ以上に分解できる場合のことである。
下表では、{支店} -> {在庫商品}、{支店} -> {メーカー}、{在庫商品} -> {メーカー}と3つの関係を含んでいるため、3つに分解可能である。
| 支店 | 在庫商品 | メーカー |
|---|---|---|
| 東京 | テレビ | A社 |
| 東京 | テレビ | B社 |
| 東京 | エアコン | A社 |
| 愛知 | 冷蔵庫 | C社 |
|
|
|
第5正規形の手順
https://ja.wikipedia.org/wiki/%E9%96%A2%E4%BF%82%E3%81%AE%E6%AD%A3%E8%A6%8F%E5%8C%96