「線形代数の基礎 - 変換行列」の版間の差分
| (同じ利用者による、間の5版が非表示) | |||
| 6行目: | 6行目: | ||
N次元空間における回転行列は、実数を成分とする正方行列であり、行列式が1のN次直交行列として特徴付けられる。<br> | N次元空間における回転行列は、実数を成分とする正方行列であり、行列式が1のN次直交行列として特徴付けられる。<br> | ||
<math>{}^t\!R =R^{-1} ,\;\det R=1.</math><br> | <math>{}^t\!R =R^{-1} ,\;\det R=1.</math><br> | ||
<br><br> | |||
== 等倍・偏倍行列 == | |||
ユークリッド空間の2次元空間および3次元空間では、等倍・偏倍行列は、以下の形で表すことができる。<br> | |||
<math> | |||
A = \begin{pmatrix} | |||
a & 0 \\ | |||
0 & b | |||
\end{pmatrix} | |||
</math><br> | |||
<br> | |||
<math> | |||
A = \begin{pmatrix} | |||
a & 0 & 0 \\ | |||
0 & b & 0 \\ | |||
0 & 0 & c | |||
\end{pmatrix} | |||
</math><br> | |||
<br><br> | |||
== 反転行列 == | |||
ユークリッド空間の2次元空間では、x軸まわりおよびy軸まわりの反転行列は、以下の形で表すことができる。<br> | |||
<math> | |||
A(\mbox{x 軸 ま わ り }) = \begin{pmatrix} | |||
-1 & 0 \\ | |||
0 & 1 | |||
\end{pmatrix} | |||
\qquad | |||
A(\mbox{y 軸 ま わ り }) = \begin{pmatrix} | |||
1 & 0 \\ | |||
0 & -1 | |||
\end{pmatrix} | |||
</math><br> | |||
<br> | |||
ユークリッド空間の3次元空間では、x軸まわり、y軸まわり、z軸まわりの反転行列は、以下の形で表すことができる。<br> | |||
<math> | |||
A(\mbox{x 軸 ま わ り }) = \begin{pmatrix} | |||
-1 & 0 & 0 \\ | |||
0 & 1 & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | |||
\qquad | |||
A(\mbox{y 軸 ま わ り }) = \begin{pmatrix} | |||
1 & 0 & 0 \\ | |||
0 & -1 & 0 \\ | |||
0 & 0 & 1 | |||
\end{pmatrix} | |||
\qquad | |||
A(\mbox{z 軸 ま わ り }) = \begin{pmatrix} | |||
1 & 0 & 0 \\ | |||
0 & 1 & 0 \\ | |||
0 & 0 & -1 | |||
\end{pmatrix} | |||
</math><br> | |||
<br><br> | |||
== 平行移動 == | |||
ユークリッド空間の2次元空間および3次元空間では、X軸方向にT<sub>x</sub>、Y軸方向にT<sub>y</sub>だけ移動する平行移動は、以下の形で表すことができる。<br> | |||
<math> | |||
A = \begin{pmatrix} | |||
1 & 0 & T_{x} \\ | |||
0 & 1 & T_{y} | |||
\end{pmatrix} | |||
\qquad | |||
\begin{pmatrix} | |||
x' \\ | |||
y' | |||
\end{pmatrix} = \begin{pmatrix} | |||
1 & 0 & T_{x} \\ | |||
0 & 1 & T_{y} | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
x \\ | |||
y \\ | |||
1 | |||
\end{pmatrix} | |||
</math><br> | |||
<br> | |||
<math> | |||
A = \begin{pmatrix} | |||
1 & 0 & 0 & T_{x} \\ | |||
0 & 1 & 0 & T_{y} \\ | |||
0 & 0 & 1 & T_{z} | |||
\end{pmatrix} | |||
\qquad | |||
\begin{pmatrix} | |||
x' \\ | |||
y' \\ | |||
z' | |||
\end{pmatrix} = \begin{pmatrix} | |||
1 & 0 & 0 & T_{x} \\ | |||
0 & 1 & 0 & T_{y} \\ | |||
0 & 0 & 1 & T_{z} | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
x \\ | |||
y \\ | |||
z \\ | |||
1 | |||
\end{pmatrix} | |||
</math><br> | |||
<br><br> | <br><br> | ||
| 11行目: | 112行目: | ||
ユークリッド空間の2次元空間では、原点中心のθ回転(反時計回りを正)の回転行列は、以下の形で表すことができる。<br> | ユークリッド空間の2次元空間では、原点中心のθ回転(反時計回りを正)の回転行列は、以下の形で表すことができる。<br> | ||
<math> | <math> | ||
R(\theta )=\begin{ | R(\theta )=\begin{pmatrix} | ||
\cos \theta &-\sin \theta \\ | \cos \theta &-\sin \theta \\ | ||
\sin \theta &\cos \theta \\ | \sin \theta &\cos \theta \\ | ||
\end{ | \end{pmatrix} | ||
</math><br> | </math><br> | ||
<br> | <br> | ||
| 23行目: | 124行目: | ||
これを行列の積で表すと、以下のようになる。<br> | これを行列の積で表すと、以下のようになる。<br> | ||
<math> | <math> | ||
\begin{ | \begin{pmatrix} | ||
x' \\ | |||
y' | |||
\end{pmatrix} = \begin{pmatrix} | |||
\cos \theta & -\sin \theta \\ | \cos \theta & -\sin \theta \\ | ||
\sin \theta & \cos \theta | \sin \theta & \cos \theta | ||
\end{ | \end{pmatrix} | ||
\begin{ | \begin{pmatrix} | ||
x \\ | |||
y | |||
\end{pmatrix} | |||
</math><br> | </math><br> | ||
<br> | <br> | ||
逆の回転は、回転角が-θとなるだけなので、<br> | 逆の回転は、回転角が-θとなるだけなので、<br> | ||
<math> | <math> | ||
R(-\theta )=\begin{ | R(-\theta )=\begin{pmatrix} | ||
\cos (-\theta) & -\sin (-\theta) \\ | \cos (-\theta) & -\sin (-\theta) \\ | ||
\sin (-\theta) & \cos (-\theta) \\ | \sin (-\theta) & \cos (-\theta) \\ | ||
\end{ | \end{pmatrix} = \begin{pmatrix} | ||
\cos \theta & \sin \theta \\ | \cos \theta & \sin \theta \\ | ||
-\sin \theta & \cos \theta \\ | -\sin \theta & \cos \theta \\ | ||
\end{ | \end{pmatrix} | ||
</math><br> | </math><br> | ||
となる。<br> | となる。<br> | ||
<br> | <br> | ||
また、回転行列には、行列の指数関数を用いた表示もある。<br> | また、回転行列には、行列の指数関数を用いた表示もある。<br> | ||
<math>R(\theta) = \exp\left(\theta \begin{ | <math>R(\theta) = \exp\left(\theta \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\right)</math><br> | ||
<br><br> | <br><br> | ||
| 50行目: | 157行目: | ||
3次元空間でのx軸、y軸、z軸周りの回転を表す回転行列は、それぞれ以下の通りである。<br> | 3次元空間でのx軸、y軸、z軸周りの回転を表す回転行列は、それぞれ以下の通りである。<br> | ||
<math> | <math> | ||
R_x (\theta )=\begin{ | R_x (\theta )=\begin{pmatrix} | ||
1 &0 &0 \\ | 1 &0 &0 \\ | ||
0 &\cos \theta &-\sin \theta \\ | 0 &\cos \theta &-\sin \theta \\ | ||
0 &\sin \theta &\cos \theta \\ | 0 &\sin \theta &\cos \theta \\ | ||
\end{ | \end{pmatrix} | ||
</math><br> | </math><br> | ||
<br> | <br> | ||
<math> | <math> | ||
R_y (\theta ) = \begin{ | R_y (\theta ) = \begin{pmatrix} | ||
\cos \theta &0 &\sin \theta \\ | \cos \theta &0 &\sin \theta \\ | ||
0 & 1 & 0 \\ | 0 & 1 & 0 \\ | ||
-\sin \theta &0 &\cos \theta \\ | -\sin \theta &0 &\cos \theta \\ | ||
\end{ | \end{pmatrix} | ||
</math><br> | </math><br> | ||
<br> | <br> | ||
<math> | <math> | ||
R_z (\theta ) = \begin{ | R_z (\theta ) = \begin{pmatrix} | ||
\cos \theta &-\sin \theta &0 \\ | \cos \theta &-\sin \theta &0 \\ | ||
\sin \theta &\cos \theta &0 \\ | \sin \theta &\cos \theta &0 \\ | ||
0 &0 &1 | 0 &0 &1 | ||
\end{ | \end{pmatrix} | ||
</math><br> | </math><br> | ||
<br> | <br> | ||
| 81行目: | 188行目: | ||
<math>R_z (\gamma ) R_x (\beta ) R_y (\alpha )</math><br> | <math>R_z (\gamma ) R_x (\beta ) R_y (\alpha )</math><br> | ||
<br><br> | <br><br> | ||
== スキュー (せん断) == | |||
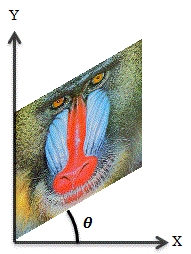
四角形を平行四辺形に変形する処理をスキュー(せん断)と呼ぶ。<br> | |||
<math> | |||
A = \begin{pmatrix} | |||
1 & 0 \\ | |||
\tan \theta & 1 | |||
\end{pmatrix} | |||
\qquad | |||
\begin{pmatrix} | |||
x' \\ | |||
y' | |||
\end{pmatrix} = \begin{pmatrix} | |||
1 & 0 \\ | |||
\tan \theta & 1 | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
x \\ | |||
y | |||
\end{pmatrix} | |||
</math><br> | |||
[[ファイル:LinearAlgebra Transformation Matrix 1.jpg|フレームなし|中央]] | |||
<br> | |||
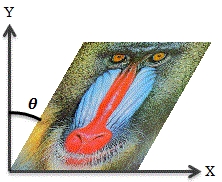
<math> | |||
A = \begin{pmatrix} | |||
1 & \tan \theta \\ | |||
0 & 1 | |||
\end{pmatrix} | |||
\qquad | |||
\begin{pmatrix} | |||
x' \\ | |||
y' | |||
\end{pmatrix} = \begin{pmatrix} | |||
1 & \tan \theta \\ | |||
0 & 1 | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
x \\ | |||
y | |||
\end{pmatrix} | |||
</math><br> | |||
[[ファイル:LinearAlgebra Transformation Matrix 2.jpg|フレームなし|中央]] | |||
<br><br> | |||
{{#seo: | |||
|title={{PAGENAME}} : Exploring Electronics and SUSE Linux | MochiuWiki | |||
|keywords=MochiuWiki,Mochiu,Wiki,Mochiu Wiki,Electric Circuit,Electric,pcb,Mathematics,AVR,TI,STMicro,AVR,ATmega,MSP430,STM,Arduino,Xilinx,FPGA,Verilog,HDL,PinePhone,Pine Phone,Raspberry,Raspberry Pi,C,C++,C#,Qt,Qml,MFC,Shell,Bash,Zsh,Fish,SUSE,SLE,Suse Enterprise,Suse Linux,openSUSE,open SUSE,Leap,Linux,uCLnux,Podman,電気回路,電子回路,基板,プリント基板 | |||
|description={{PAGENAME}} - 電子回路とSUSE Linuxに関する情報 | This page is {{PAGENAME}} in our wiki about electronic circuits and SUSE Linux | |||
|image=/resources/assets/MochiuLogo_Single_Blue.png | |||
}} | |||
__FORCETOC__ | __FORCETOC__ | ||
[[カテゴリ:線形代数]] | [[カテゴリ:線形代数]] | ||
2024年11月1日 (金) 04:16時点における最新版
概要
線形代数において、回転行列とは、ユークリッド空間内における原点中心の回転変換の表現行列のことである。
2次元や3次元では、幾何学、物理学、コンピュータグラフィックスの分野での計算によく使用される。
N次元空間における回転行列は、実数を成分とする正方行列であり、行列式が1のN次直交行列として特徴付けられる。
等倍・偏倍行列
ユークリッド空間の2次元空間および3次元空間では、等倍・偏倍行列は、以下の形で表すことができる。
反転行列
ユークリッド空間の2次元空間では、x軸まわりおよびy軸まわりの反転行列は、以下の形で表すことができる。
ユークリッド空間の3次元空間では、x軸まわり、y軸まわり、z軸まわりの反転行列は、以下の形で表すことができる。
平行移動
ユークリッド空間の2次元空間および3次元空間では、X軸方向にTx、Y軸方向にTyだけ移動する平行移動は、以下の形で表すことができる。
2次元の回転行列
ユークリッド空間の2次元空間では、原点中心のθ回転(反時計回りを正)の回転行列は、以下の形で表すことができる。
これは、原点中心にθ回転して点(x, y)が(x', y')に写る時、図形的考察または加法定理より、x', y'は以下のように表される。
これを行列の積で表すと、以下のようになる。
逆の回転は、回転角が-θとなるだけなので、
となる。
また、回転行列には、行列の指数関数を用いた表示もある。
3次元の回転行列
各軸周りの回転
3次元空間でのx軸、y軸、z軸周りの回転を表す回転行列は、それぞれ以下の通りである。
回転の方向において、Rxはy軸をz軸に向ける方向、Ryはz軸をx軸に向ける方向、Rzはx軸をy軸に向ける方向である。
オイラー角
一般の回転行列も、これら3つの各軸周りの回転行列Rx、Ry、Rzの積により得ることができる。
例えば、以下の積は、yxz系で表したときのオイラー角がα、β、γであるような回転を表す。
スキュー (せん断)
四角形を平行四辺形に変形する処理をスキュー(せん断)と呼ぶ。